Exam 6: Normal Probability Distributions
Exam 1: Introduction to Statistics106 Questions
Exam 2: Summarizing and Graphing Data85 Questions
Exam 3: Statistics for Describing, Exploring, and Comparing Data187 Questions
Exam 4: Probability186 Questions
Exam 5: Discrete Probability Distributions155 Questions
Exam 6: Normal Probability Distributions227 Questions
Exam 7: Estimates and Sample Size141 Questions
Exam 8: Hypothesis Testing139 Questions
Exam 9: Inferences From Two Samples133 Questions
Exam 10: Correlation and Regression104 Questions
Exam 11: Chi-Square and Analysis of Variance65 Questions
Select questions type
A population consists of these values: . Find the mean, , and standard deviation, , of the population. List all samples of size that are obtained without replacement. Find the population of all values of by finding the mean of each sample that you listed. Find the mean and standard deviation for the population of sample means by using the formulas:
(Essay)
4.9/5  (33)
(33)
The Precision Scientific Instrument Company manufactures thermometers that are supposed to give readings of 0°C at the freezing point of water. Tests on a large sample of these thermometers reveal that at the freezing point of water, some give readings below 0°C (denoted by negative numbers) and some give readings above 0°C (denoted by positive numbers). Assume that the mean reading is 0°C and the standard deviation of the readings is 1.00°C. Also assume that the frequency distribution of errors closely resembles the normal distribution. A thermometer is randomly selected and tested. Find the temperature reading corresponding to the given information.
-A quality control analyst wants to examine thermometers that give readings in the bottom 4%. Find the reading that separates the bottom 4% from the others.
(Multiple Choice)
4.7/5  (38)
(38)
Using the following uniform density curve, answer the question. 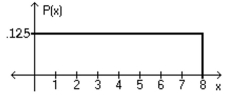 -What is the probability that the random variable has a value between 2.3 and 5?
-What is the probability that the random variable has a value between 2.3 and 5?
(Multiple Choice)
4.8/5  (40)
(40)
Estimate the indicated probability by using the normal distribution as an approximation to the binomial distribution.
-Two percent of hair dryers produced in a certain plant are defective. Estimate the probability that of 10,000 randomly selected hair dryers, exactly 225 are defective.
(Multiple Choice)
4.8/5  (33)
(33)
Assume that the weights of quarters are normally distributed with a mean of 5.67 g and a standard deviation 0.070 g. A vending machine will only accept coins weighing between 5.48 g and 5.82 g.
What percentage of legal quarters will be rejected?
(Multiple Choice)
4.9/5  (43)
(43)
Personal phone calls received in the last three days by a new employee were 2, 5, and 7. Assume that samples of size 2 are randomly selected with replacement from this population of three values. List the different possible samples, and find the mean of each of them.
(Essay)
4.9/5  (44)
(44)
If selecting samples of si from a population with a known mean and standard deviation,what requirement, if any, must be satisfied in order to assume that the distribution of the sample means is a normal distribution?
(Multiple Choice)
4.9/5  (46)
(46)
Scores on a test are normally distributed with a mean of 68.9 and a standard deviation of 11.6. Find P81, which separates the bottom 81% from the top 19%.
(Multiple Choice)
4.9/5  (40)
(40)
Explain how a nonstandard normal distribution differs from the standard normal distribution. Describe the process for finding probabilities for nonstandard normal distributions.
(Essay)
4.8/5  (34)
(34)
Find the indicated z score. The graph depicts the standard normal distribution with mean 0 and standard deviation 1.
-Shaded area is 0.0694. 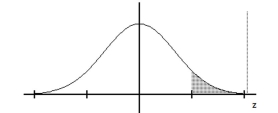
(Multiple Choice)
5.0/5  (43)
(43)
For a standard normal distribution, find the percentage of data that are more than 1 standard deviation away from the mean.
(Multiple Choice)
4.8/5  (44)
(44)
SAT verbal scores are normally distributed with a mean of 430 and a standard deviation of 120 (based on the data from the College Board ATP). If a sample of 15 students is selected randomly, find the probability that the sample mean is above 500. Does the central limit theorem apply for this problem?
(Essay)
4.9/5  (33)
(33)
Examine the given data set and determine whether the requirement of a normal distribution is satisfied. Assume that the requirement for a normal distribution is loose in the sense that the population distribution need not be exactly normal, but it must have a distribution which is basically symmetric with only one mode. Explain why you do or do not think that the requirement is satisfied.
-The data below represents the amount of television watched per week (in hours) for 40 randomly selected teenagers.
13 4 17 14 9 6 7 5 14 12 20 16 0 15 10 6 5 3 13 14 15 5 3 5 8 11 12 13 14 7 4 6 9 13 3 14 24 15 17 20
(Essay)
4.9/5  (41)
(41)
For the binomial distribution with the given values for n and p, state whether or not it is suitable to use the normal distribution as an approximation.
-
(Multiple Choice)
4.8/5  (38)
(38)
For women aged 18-24, systolic blood pressures (in mm Hg) are normally distributed with a mean of 114.8 and a standard deviation of 13.1. If 23 women aged 18-24 are randomly selected, find the probability that their mean systolic blood pressure is between 119 and 122.
(Multiple Choice)
4.9/5  (28)
(28)
Suppose that replacement times for washing machines are normally distributed with a mean of 10.9 years and a standard deviation of 1 years. Find the replacement time that separates the top 18% from the bottom 82%.
(Multiple Choice)
5.0/5  (37)
(37)
Examine the given data set and determine whether the requirement of a normal distribution is satisfied. Assume that the requirement for a normal distribution is loose in the sense that the population distribution need not be exactly normal, but it must have a distribution which is basically symmetric with only one mode. Explain why you do or do not think that the requirement is satisfied.
-The amount of rainfall (in inches) in 25 consecutive years in a certain city. 20.4 25.1 22.8 27.0 23.5
24.2 26.0 25.6 23.3 24.1
21.9 27.6 24.7 25.3 21.6
31.0 23.6 26.1 25.5 24.8
18.1 22.4 24.9 30.0 29.3
(Essay)
4.7/5  (42)
(42)
Scores on an English test are normally distributed with a mean of 37.4 and a standard deviation of 7.9. Find the score that separates the top 59% from the bottom 41%
(Multiple Choice)
4.9/5  (36)
(36)
Lengths of pregnancies are normally distributed with a mean of 268 days and a standard deviation of 15 days. (a) Find the probability of a pregnancy lasting more than 250 days. (b) Find the probability of a pregnancy lasting more than 280 days. Draw the diagram for each and discuss the part of the solution that would be different to finding the requested probabilities.
(Essay)
4.9/5  (46)
(46)
The weights of certain machine components are normally distributed with a mean of 8.6 g and a standard deviation of 0.06 g. Find the two weights that separate the top 3% and the bottom 3%. these weights could serve as limits used to identify which components should be rejected. Round to the nearest hundredth of a gram.
(Multiple Choice)
4.7/5  (31)
(31)
Showing 21 - 40 of 227
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)