Exam 6: Inverse Circular Functions and Trigonometric Equations
Exam 1: Trigonometric Functions188 Questions
Exam 2: Acute Angles and Right Triangles204 Questions
Exam 3: Radian Measure and the Unit Circle167 Questions
Exam 4: Graphs of the Circular Functions137 Questions
Exam 5: Trigonometric Identities321 Questions
Exam 6: Inverse Circular Functions and Trigonometric Equations179 Questions
Exam 7: Applications of Trigonometry and Vectors103 Questions
Exam 8: Complex Numbers, Polar Equations, and Parametric Equations60 Questions
Select questions type
Solve.
-Consider the formula T = 591 - 76 cos 2ϴ, where ϴ is measured in degrees. To the nearest hundredth of a degree, what is the smallest positive value of ϴ for which the value of T will be 577?
(Multiple Choice)
4.9/5  (35)
(35)
Use the parallelogram rule to find the magnitude of the resultant force for the two forces shown in the figure. Round to
one decimal place.
-Explain what is wrong with the following solution for the equation in the interval ).
(Essay)
4.9/5  (31)
(31)
Solve the equation for x, where x is restricted to the given interval.
-
(Multiple Choice)
4.9/5  (32)
(32)
Solve the equation for solutions in the interval [0°, 360°). Round to the nearest degree.
-
(Multiple Choice)
4.9/5  (37)
(37)
33 Solve the equation for solutions over the interval . Write solutions as exact values or to four decimal places, as appropriate.
-
(Multiple Choice)
4.9/5  (32)
(32)
Use the parallelogram rule to find the magnitude of the resultant force for the two forces shown in the figure. Round to
one decimal place.
-On the given graph of sketch the graph of as defined in the text. Give the domain and the range.
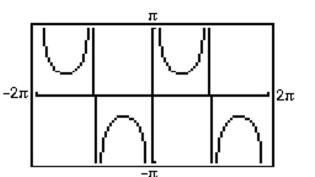
(Essay)
4.8/5  (35)
(35)
Use a calculator to give the value to the nearest degree.
-
(Multiple Choice)
4.9/5  (34)
(34)
Use a calculator to find the value. Give answers as real numbers and round to 4 decimal places, if necessary.
-
(Multiple Choice)
4.8/5  (31)
(31)
Solve the equation (x in radians and in degrees) for all exact solutions where appropriate. Round approximate answers
in radians to four decimal places and approximate answers in degrees to the nearest tenth.
-
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-It can be shown that if the angle of elevation from an observer to the top of an object is A and the angle of elevation d ft closer is B, then the height of the object is given by
Find if , and . Give your answer in degrees to the nearest hundredth.
(Multiple Choice)
4.8/5  (44)
(44)
Showing 81 - 100 of 179
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)