Exam 6: Inverse Circular Functions and Trigonometric Equations
Exam 1: Trigonometric Functions188 Questions
Exam 2: Acute Angles and Right Triangles204 Questions
Exam 3: Radian Measure and the Unit Circle167 Questions
Exam 4: Graphs of the Circular Functions137 Questions
Exam 5: Trigonometric Identities321 Questions
Exam 6: Inverse Circular Functions and Trigonometric Equations179 Questions
Exam 7: Applications of Trigonometry and Vectors103 Questions
Exam 8: Complex Numbers, Polar Equations, and Parametric Equations60 Questions
Select questions type
Solve the problem.
-A painting 1 meter high and 3 meters from the floor will cut off an angle to an observer, where , assuming that the observer is feet from the wall where the painting is displayed and that the eyes of the observer are meters above the ground (see the figure). Find the value of for . Round to the nearest tenth of a degree.
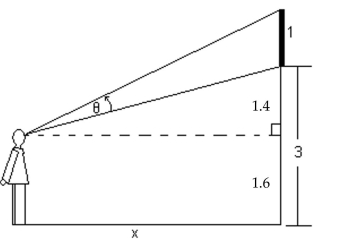
(Multiple Choice)
4.8/5  (32)
(32)
Use the parallelogram rule to find the magnitude of the resultant force for the two forces shown in the figure. Round to
one decimal place.
-Explain what is wrong with the following solution for the equation in the interval .
(Essay)
4.8/5  (37)
(37)
Use a calculator to give the real number value. Round the answer to 7 decimal places.
-
(Multiple Choice)
4.7/5  (38)
(38)
Solve the problem.
-The formula for the up-and-down motion of a weight on a spring is given by
where a is the radius of the circle, is the spring constant, is the mass, and is the time. Solve the equation for t.
(Multiple Choice)
4.8/5  (37)
(37)
Use a calculator to give the real number value. Round the answer to 7 decimal places.
-
(Multiple Choice)
5.0/5  (40)
(40)
Use a calculator to find the value. Give answers as real numbers and round to 4 decimal places, if necessary.
-
(Multiple Choice)
5.0/5  (29)
(29)
Solve the equation for x, where x is restricted to the given interval.
-
(Multiple Choice)
4.7/5  (40)
(40)
Solve.
-The output voltage for an generator is approximated by . Find the smallest positive value of for which the output is 75 volts. Round values to 4 decimal places.
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-The position of a weight on a spring relative to the point of equilibrium is given by y = 4 cos 6t - 2 sin 6t,
Where the arguments are in radians and t is in seconds. Find the smallest value of t for which the
Weight is at the point of equilibrium (y = 0). Give your answer to the nearest hundredth.
(Multiple Choice)
4.8/5  (33)
(33)
Solve the equation for exact solutions over the interval [0, 2
-
(Multiple Choice)
4.7/5  (24)
(24)
Solve the equation for exact solutions over the interval [0, 2
-
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem.
-The figure shows a stationary spy satellite positioned 12,000 miles above the equator. What percent, to the nearest tenth, of the equator can be seen from the satellite? The diameter of Earth is 7927
Miles at the equator. 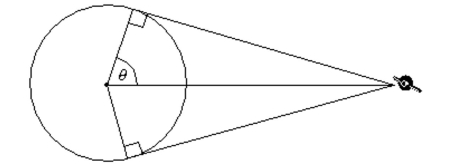
(Multiple Choice)
4.9/5  (40)
(40)
Showing 161 - 179 of 179
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)