Exam 2: Functions
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Solve the problem.
-The accompanying figure shows the graph of shifted to a new position. Write the equation for the new graph.
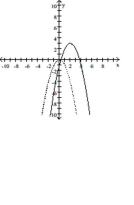
(Multiple Choice)
4.9/5  (44)
(44)
Find the domain and range of the inverse of the given function.
-
(Multiple Choice)
4.7/5  (37)
(37)
Express the following logarithm as specified.
- in terms of and
(Multiple Choice)
4.9/5  (49)
(49)
Provide an appropriate response.
Consider the function y Can x be greater than 1?
-
(True/False)
4.7/5  (40)
(40)
Use a graphing calculator or computer to determine which of the given viewing windows displays the most appropriate
graph of the specified function.
-
(Multiple Choice)
4.9/5  (46)
(46)
Solve the problem.
-The kinetic energy K of a mass is proportional to the square of its velocity v. If K = 4320 joules when v = 12 m/sec, what is K when v = 8 m/sec?
(Multiple Choice)
4.7/5  (26)
(26)
Assume that f is an even function, g is an odd function, and both f and g are defined on the entire real line. State whether
the combination of functions (where defined) is even or odd.
-
(Multiple Choice)
4.8/5  (34)
(34)
Showing 181 - 200 of 413
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)