Exam 2: Functions
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
One of sin x, cos x, and tan x is given. Find the other two if x lies in the specified interval.
-
(Multiple Choice)
4.8/5  (33)
(33)
The problem tells how many units and in what direction the graph of the given equation is to be shifted. Give an
equation for the shifted graph. Then sketch the original graph with a dashed line and the shifted graph with a solid line.
-
Down 5 , right 6
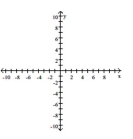
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-The accompanying figure shows the graph of shifted to a new position. Write the equation for the new graph.
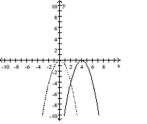
(Multiple Choice)
4.8/5  (37)
(37)
Consider the function y Can x be 0?
-What is the domain of the function ?
(Multiple Choice)
4.7/5  (40)
(40)
Find the formula for the function.
-A point P in the fourth quadrant lies on the graph of the function f(x) . Express the slope of the line joining P to the origin as a function of x.
(Multiple Choice)
4.8/5  (37)
(37)
Graph the function. Specify the intervals over which the function is increasing and the intervals where it is decreasing.
-
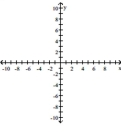
(Multiple Choice)
4.8/5  (39)
(39)
Assume that f is an even function, g is an odd function, and both f and g are defined on the entire real line. State whether
the combination of functions (where defined) is even or odd.
-
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-How long will it take for prices in the economy to double at a 12% annual inflation rate? Round the answer to the nearest hundredth.
(Multiple Choice)
4.7/5  (38)
(38)
Use the laws of exponents to simplify. Do not use negative exponents in your answer.
-
(Multiple Choice)
4.8/5  (24)
(24)
One of sin x, cos x, and tan x is given. Find the other two if x lies in the specified interval.
- in
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-Graph the functions and together with their sum, product, two differences, and two quotients.
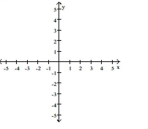
(Essay)
4.9/5  (49)
(49)
Showing 161 - 180 of 413
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)