Exam 5: Analytic Trigonometry

Solve the problem. -A parallelogram has sides of length $35.8 \mathrm {~cm}$ and $16.1 \mathrm {~cm}$ . If the longer diagonal has a length of $37.9 \mathrm {~cm}$ , what is the angle opposite this diagonal? Give your answer to the nearest tenth of a degree.

Write the expression as the sine, cosine, or tangent of an angle. - $\sin 31 ^ { \circ } \cos 28 ^ { \circ } - \cos 31 ^ { \circ } \sin 28 ^ { \circ }$

Prove the identity. - $\sin ^ { 3 } x \cos ^ { 2 } x = \sin x \left( \cos ^ { 2 } x - \cos ^ { 4 } x \right)$

Provide an appropriate response. - $\text { A student writes "tan } 2 + 1 = \sec ^ { 2 } \text {." Comment on this student's work. }$

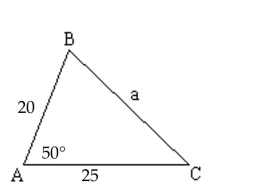
The given measurements may or may not determine a triangle. If not, then state that no triangle is formed. If a triangle is formed, then use the Law of Sines to solve the triangle, if it is possible, or state that the Law of Sines cannot be used. -

Solve the triangle. - $\mathrm { a } = 3.3 , \mathrm {~b} = 7.7 , \mathrm { c } = 6.6$

Solve the problem. -An airplane leaves an airport and flies due west 170 miles and then 160 miles in the direction S 79.50°W. How far is the plane from the airport at this time (to the nearest mile)?

The given measurements may or may not determine a triangle. If not, then state that no triangle is formed. If a triangle is formed, then use the Law of Sines to solve the triangle, if it is possible, or state that the Law of Sines cannot be used. - $\mathrm { B } = 107 ^ { \circ } , \mathrm { c } = 9 , \mathrm {~b} = 11$

Match the graph with the correct equation. -

Find an exact value. - $\sin 15 ^ { \circ }$

Match the graph with the correct equation. -

Provide an appropriate response. -Graph the expression $\sec ^ { 2 } x - \sec ^ { 2 } x \sin ^ { 2 } x$ on your calculator. Determine what constant or single circular function is equivalent to the given expression.

Prove the identity. - $\sin ^ { 3 } 3 x = \frac { 1 } { 2 } ( \sin 3 x ) ( 1 - \cos 6 x )$

Prove the identity. - $\sin \left( x + \frac { \pi } { 2 } \right) = \cos x$

Find all solutions to the equation. - $\cos ^ { 2 } x = 0.8$ (Use a calculator. Express your answer in radians as a decimal rounded to the nearest thousandth.)

Explain why the law of sines cannot be used to solve a triangle if we are given the lengths of two sides and the measure of the included angle.

Find all solutions in the interval [0, 2π] - $\cos ^ { 2 } x + 2 \cos x + 1 = 0$

Find the exact value by using a half-angle identity. - $\tan 165 ^ { \circ }$

Simplify the expression. - $\frac { \sin ^ { 2 } x - 1 } { \cos ( - x ) }$

Rewrite with only sin x and cos x. - $\sin 3 x + \cos 3 x$