Exam 5: Analytic Trigonometry
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Find all solutions to the equation in the interval [0, 2).
-
(Multiple Choice)
4.7/5  (38)
(38)
State whether the given measurements determine zero, one, or two triangles.
-
(Multiple Choice)
4.8/5  (34)
(34)
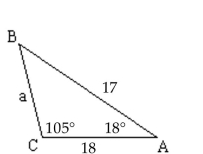
The given measurements may or may not determine a triangle. If not, then state that no triangle is formed. If a triangle is
formed, then use the Law of Sines to solve the triangle, if it is possible, or state that the Law of Sines cannot be used.
-
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-A building has a ramp to its front doors to accommodate the handicapped. If the distance from the building to the end of the ramp is 13 feet and the height from the ground to the front doors is 4 feet, how long is the ramp?
(Round to the nearest tenth.)
(Multiple Choice)
4.9/5  (40)
(40)
Write the expression as the sine, cosine, or tangent of an angle.
-
(Multiple Choice)
4.8/5  (37)
(37)
Write each expression in factored form as an algebraic expression of a single trigonometric function.
-
(Multiple Choice)
5.0/5  (39)
(39)
Find the area. Round your answer to the nearest hundredth if necessary.
-Find the area of the triangle with the following measurements:
(Multiple Choice)
4.8/5  (40)
(40)
Two triangles can be formed using the given measurements. Solve both triangles.
-
(Multiple Choice)
4.9/5  (33)
(33)
Given the SSS parts of a triangle, is it better to use the law of sines or the law of cosines as the first step in
solving the triangle? Explain.
(Essay)
4.9/5  (44)
(44)
Find all solutions to the equation.
- (Express your answer in radians, in exact form.)
(Multiple Choice)
4.8/5  (34)
(34)
Showing 241 - 260 of 313
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)