Exam 1: Functions and Graphs
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Find f(x) and g(x) so that the function can be described as y = f(g(x)).
-
(Multiple Choice)
4.8/5  (36)
(36)
Give the equation of the function g whose graph is described.
-The graph of is reflected across the -axis .
(Multiple Choice)
4.7/5  (36)
(36)
Solve the problem.
-Use the graph of to estimate the local maximum and local minimum.
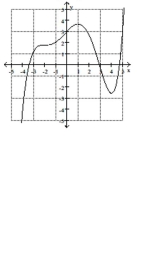
(Multiple Choice)
4.8/5  (39)
(39)
Choose the one alternative that best completes the statement or answers the question.
Write a mathematical expression for the quantity described verbally.
-The total cost if plus for each item produced.
(Multiple Choice)
4.9/5  (29)
(29)
Solve the equation graphically by converting it to an equivalent equation with 0 on the right-hand side and then finding
the x-intercepts.
-
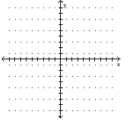
(Multiple Choice)
4.8/5  (26)
(26)
Find the (x,y) pair for the value of the parameter.
- and for
(Multiple Choice)
4.8/5  (43)
(43)
Determine whether the formula determines y as a function of x.
-
(True/False)
4.8/5  (27)
(27)
Write the specified quantity as a function of the specified variable.
-The base of an isosceles triangle is half as long as the two equal sides. Write the area of the triangle as a function of the length of the base.
(Multiple Choice)
4.8/5  (34)
(34)
Write the specified quantity as a function of the specified variable.
-The height of a right circular cylinder equals its diameter. Write the volume of the cylinder as a function of its radius.
(Multiple Choice)
4.9/5  (28)
(28)
Describe how to transform the graph of f into the graph of g.
-
(Multiple Choice)
4.8/5  (33)
(33)
Sketch the graph of y1 as a solid line or curve. Then sketch the graph of y2 as a dashed line or curve by one or more of
these: a vertical and/or horizontal shift of the graph y1, a vertical stretch or shrink of the graph of y1, or a reflection of the
graph of y1 across an axis.
-
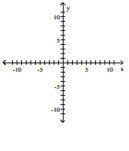
(Multiple Choice)
4.9/5  (27)
(27)
Describe how to transform the graph of f into the graph of g.
- and
(Multiple Choice)
4.7/5  (34)
(34)
Write the word or phrase that best completes each statement or answers the question.
Confirm that f and g are inverses by showing that f(g(x)) = x and g(f(x)) = x.
-
(Essay)
4.9/5  (35)
(35)
Showing 221 - 240 of 362
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)