Exam 5: Antiderivatives and Indefinite Integration
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Find the general solution of the differential equation below and check the result by differentiation.
(Multiple Choice)
4.8/5  (36)
(36)
Find the smallest n such that the error estimate from the error formula in the approximation of the definite integral is less than using the Trapezoidal Rule.
(Multiple Choice)
4.7/5  (39)
(39)
Use the properties of summation and Theorem 5.2 to evaluate the sum.
(Multiple Choice)
4.8/5  (33)
(33)
Find table lists several measurements gathered in an experiment to approximate an unknown continuous function . Approximate the integral using the Simpson's Rule. Round your answer to three decimal places.
x 0.00 0.25 0.50 0.75 1.00 1.25 1.50 1.75 2.00 y 4.72 4.77 4.82 6.17 6.52 7.17 7.32 7.97 8.02
(Multiple Choice)
4.8/5  (43)
(43)
Evaluate the following definite integral by the limit definition.
(Multiple Choice)
4.8/5  (34)
(34)
Evaluate the definite integral of a function your results.
(Multiple Choice)
4.9/5  (35)
(35)
Suppose that the probability that a person will remember between of material learned in an experiment is where represents the proportion
remembered. Determine from the figure below, the probability that a randomly chosen individual will recall between and of the material? Express your answer as a percent rounded to three decimal places.
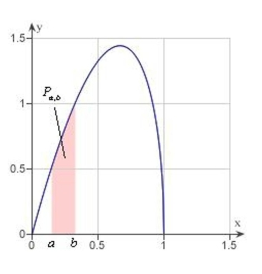
(Multiple Choice)
4.9/5  (36)
(36)
Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using 8 subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral.
(Multiple Choice)
4.7/5  (34)
(34)
Evaluate the following definite integral by the limit definition.
(Multiple Choice)
4.7/5  (35)
(35)
the square of . Time is measured in days and is the amount that remains to be disbursed. Find the amount that remains to be disbursed after 30 days. Assume that all the money will be disbursed in 100 days.
(Multiple Choice)
5.0/5  (47)
(47)
Find the general solution of the differential equation below and check the result by differentiation.
(Multiple Choice)
4.7/5  (41)
(41)
Showing 101 - 120 of 167
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)