Exam 17: Multiple Regression
Exam 1: What Is Statistics41 Questions
Exam 2: Graphical and Tabular Descriptive Techniques199 Questions
Exam 3: Numerical Descriptive Techniques226 Questions
Exam 4: Data Collection and Sampling82 Questions
Exam 5: Probability212 Questions
Exam 6: Random Variables and Discrete Probability Distributions174 Questions
Exam 7: Continuous Probability Distributions167 Questions
Exam 8: Sampling Distributions133 Questions
Exam 9: Introduction to Estimation88 Questions
Exam 10: Introduction to Hypothesis Testing186 Questions
Exam 11: Inference About a Population76 Questions
Exam 12: Inference About Comparing Two Populat85 Questions
Exam 13: Inference About Comparing Two Populat85 Questions
Exam 14: Analysis of Variance127 Questions
Exam 15: Chi-Squared Tests118 Questions
Exam 16: Simple Linear Regression and Correlat238 Questions
Exam 17: Multiple Regression147 Questions
Exam 18: Review of Statistical Inference189 Questions
Select questions type
Three predictor variables are being considered for use in a linear regression model. Given the correlation matrix below, does it appear that multicollinearity could be a problem? 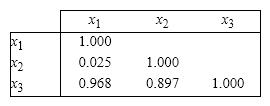
(Essay)
4.8/5  (26)
(26)
In testing the validity of a multiple regression model in which there are four independent variables, the null hypothesis is:
(Multiple Choice)
4.9/5  (35)
(35)
Student's Final Grade A statistics professor investigated some of the factors that affect an individual student's final grade in her course. She proposed the multiple regression model 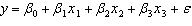 , where y is the final grade (out of 100 points), x 1 is the number of lectures skipped, x 2 is the number of late assignments, and x 3 is the midterm exam score (out of 100). The professor recorded the data for 50 randomly selected students. The computer output is shown below. THE REGRESSION EQUATION IS
, where y is the final grade (out of 100 points), x 1 is the number of lectures skipped, x 2 is the number of late assignments, and x 3 is the midterm exam score (out of 100). The professor recorded the data for 50 randomly selected students. The computer output is shown below. THE REGRESSION EQUATION IS 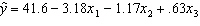
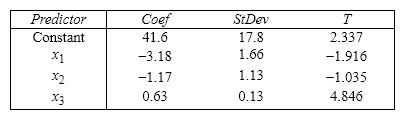 S = 13.74 R - Sq = 30.0%
S = 13.74 R - Sq = 30.0%
 {Student's Final Grade Narrative} Does this data provide enough evidence at the 1% significance level to conclude that the final grade and the midterm exam score are positively linearly related?
{Student's Final Grade Narrative} Does this data provide enough evidence at the 1% significance level to conclude that the final grade and the midterm exam score are positively linearly related?
(Essay)
4.9/5  (43)
(43)
In calculating the standard error of the estimate, 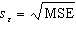 , there are ( n - k - 1)degrees of freedom, where n is the sample size and k is the number of independent variables in the model.
, there are ( n - k - 1)degrees of freedom, where n is the sample size and k is the number of independent variables in the model.
(True/False)
4.7/5  (35)
(35)
Real Estate Builder A real estate builder wishes to determine how house size is influenced by family income, family size, and education of the head of household. House size is measured in hundreds of square feet, income is measured in thousands of dollars, and education is measured in years. A partial computer output is shown below. SUMMARY OUTPUT
 ANOVA
ANOVA 
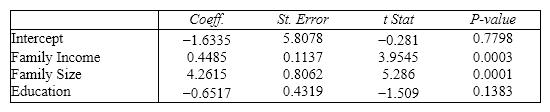 {Real Estate Builder Narrative} At the 0.01 level of significance, what conclusion should the builder draw regarding the inclusion of income in the regression model?
{Real Estate Builder Narrative} At the 0.01 level of significance, what conclusion should the builder draw regarding the inclusion of income in the regression model?
(Essay)
4.9/5  (36)
(36)
In a multiple regression model, the following statistics are given: SSE = 100, R 2 = 0.995, k = 5, and n = 15. Then, the coefficient of determination adjusted for degrees of freedom is:
(Multiple Choice)
4.9/5  (41)
(41)
Student's Final Grade A statistics professor investigated some of the factors that affect an individual student's final grade in her course. She proposed the multiple regression model 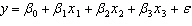 , where y is the final grade (out of 100 points), x 1 is the number of lectures skipped, x 2 is the number of late assignments, and x 3 is the midterm exam score (out of 100). The professor recorded the data for 50 randomly selected students. The computer output is shown below. THE REGRESSION EQUATION IS
, where y is the final grade (out of 100 points), x 1 is the number of lectures skipped, x 2 is the number of late assignments, and x 3 is the midterm exam score (out of 100). The professor recorded the data for 50 randomly selected students. The computer output is shown below. THE REGRESSION EQUATION IS 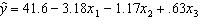
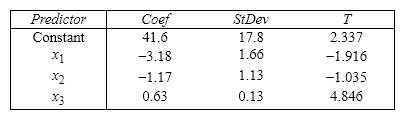 S = 13.74 R - Sq = 30.0%
S = 13.74 R - Sq = 30.0%  {Student's Final Grade Narrative} Does this data provide enough evidence to conclude at the 5% significance level that the model is useful in predicting the final grade?
{Student's Final Grade Narrative} Does this data provide enough evidence to conclude at the 5% significance level that the model is useful in predicting the final grade?
(Essay)
4.8/5  (37)
(37)
For the following multiple regression model: 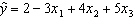 , a unit increase in x 1, holding x 2 and x 3 constant, results in:
, a unit increase in x 1, holding x 2 and x 3 constant, results in:
(Multiple Choice)
4.8/5  (40)
(40)
In a multiple regression analysis involving 6 independent variables, the total variation in y is 900 and SSR = 600. What is the value of SSE?
(Multiple Choice)
4.8/5  (32)
(32)
For a multiple regression model the following statistics are given: Total variation in y = 250, SSE = 50, k = 4, and n = 20. Then, the coefficient of determination adjusted for the degrees of freedom is:
(Multiple Choice)
4.8/5  (41)
(41)
When an additional explanatory variable is introduced into a multiple regression model, coefficient of determination adjusted for degrees of freedom can never decrease.
(True/False)
4.8/5  (35)
(35)
Most statistical software print a second R 2 statistic, called the coefficient of determination adjusted for degrees of freedom, which has been adjusted to take into account the sample size and the number of independent variables.
(True/False)
4.8/5  (36)
(36)
Real Estate Builder A real estate builder wishes to determine how house size is influenced by family income, family size, and education of the head of household. House size is measured in hundreds of square feet, income is measured in thousands of dollars, and education is measured in years. A partial computer output is shown below. SUMMARY OUTPUT
 ANOVA
ANOVA 
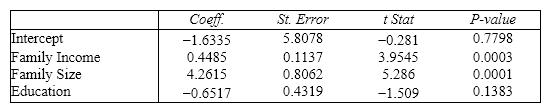 {Real Estate Builder Narrative} When the builder used a simple linear regression model with house size as the dependent variable and education as the independent variable, he obtained an R-square value of 23.0%. What additional percentage of the total variation in house size has been explained by including family size and income in the multiple regression?
{Real Estate Builder Narrative} When the builder used a simple linear regression model with house size as the dependent variable and education as the independent variable, he obtained an R-square value of 23.0%. What additional percentage of the total variation in house size has been explained by including family size and income in the multiple regression?
(Essay)
4.9/5  (32)
(32)
The validity of a multiple regression model is tested using a(n)_________ test.
(Short Answer)
4.9/5  (36)
(36)
A multiple regression model has the form: 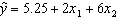 . As x 2 increases by one unit, holding x 1 constant, then the value of y will increase by:
. As x 2 increases by one unit, holding x 1 constant, then the value of y will increase by:
(Multiple Choice)
4.7/5  (26)
(26)
Multicollinearity affects the t -tests of the individual coefficients as well as the F -test in the analysis of variance for regression because the F -test combines the t -tests into a single test.
(True/False)
4.8/5  (36)
(36)
Real Estate Builder A real estate builder wishes to determine how house size is influenced by family income, family size, and education of the head of household. House size is measured in hundreds of square feet, income is measured in thousands of dollars, and education is measured in years. A partial computer output is shown below. SUMMARY OUTPUT  ANOVA
ANOVA

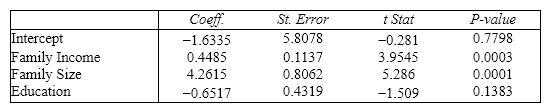 {Real Estate Builder Narrative} What is the value of the calculated F -test statistic that is missing from the output for testing whether the whole regression model is significant?
{Real Estate Builder Narrative} What is the value of the calculated F -test statistic that is missing from the output for testing whether the whole regression model is significant?
(Essay)
4.9/5  (37)
(37)
Real Estate Builder A real estate builder wishes to determine how house size is influenced by family income, family size, and education of the head of household. House size is measured in hundreds of square feet, income is measured in thousands of dollars, and education is measured in years. A partial computer output is shown below. SUMMARY OUTPUT
 ANOVA
ANOVA

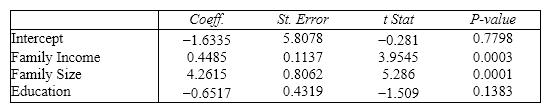 {Real Estate Builder Narrative} Which of the following values for the level of significance is the smallest for which at least two explanatory variables are significant individually: a = .01, .05, .10, and .15?
{Real Estate Builder Narrative} Which of the following values for the level of significance is the smallest for which at least two explanatory variables are significant individually: a = .01, .05, .10, and .15?
(Essay)
4.8/5  (32)
(32)
In order to test the validity of a multiple regression model involving 5 independent variables and 30 observations, the numerator and denominator degrees of freedom for the critical value of F are, respectively,
(Multiple Choice)
4.8/5  (24)
(24)
Showing 101 - 120 of 147
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)