Exam 16: Polygons
Exam 1: Reasoning About Quantities34 Questions
Exam 2: Numeration Systems96 Questions
Exam 3: Understanding Whole Number Operations66 Questions
Exam 4: Some Conventional Ways of Computing17 Questions
Exam 5: Using Numbers in Sensible Ways38 Questions
Exam 6: Meanings for Fractions85 Questions
Exam 7: Computing With Fractions54 Questions
Exam 8: Multiplicative Comparisons and Multiplicative Reasoning19 Questions
Exam 9: Ratios, Rates, Proportions, and Percents33 Questions
Exam 10: Integers and Other Number Systems24 Questions
Exam 11: Number Theory57 Questions
Exam 12: What Is Algebra28 Questions
Exam 13: A Quantitative Approach to Algebra and Graphing18 Questions
Exam 14: Understanding Change: Relationships Among Time, Distance, and Rate10 Questions
Exam 15: Further Topics in Algebra and Change55 Questions
Exam 16: Polygons75 Questions
Exam 17: Polyhedra51 Questions
Exam 18: Symmetry17 Questions
Exam 19: Tessellations9 Questions
Exam 20: Similarity47 Questions
Exam 21: Curves, Constructions, and Curved Surfaces17 Questions
Exam 22: Transformation Geometry24 Questions
Exam 23: Measurement Basics21 Questions
Exam 24: Area, Surface Area, and Volume27 Questions
Exam 25: Counting Units Fast: Measurement Formulas31 Questions
Exam 26: Special Topics in Measurement21 Questions
Exam 27: Quantifying Uncertainty39 Questions
Exam 28: Determining More Complicated Probabilities37 Questions
Exam 29: Introduction to Statistics and Sampling7 Questions
Exam 30: Representing and Interpreting Data With One Variable32 Questions
Exam 31: Dealing With Multiple Data Sets or With Multiple Variables8 Questions
Exam 32: Variability in Samples21 Questions
Exam 33: Special Topics in Probability16 Questions
Select questions type
It is possible to make a regular pyramid using an isosceles trapezoid as a base.
(True/False)
4.9/5  (32)
(32)
The sum of the measures of all of the angles of a 17-gon is _____.
(Short Answer)
4.8/5  (30)
(30)
State a fact that is true for all rectangles but not true for all parallelograms.
(Essay)
4.8/5  (35)
(35)
How many diagonals does each of these shapes have?
A) a pentagon
B) a 103-gon
(Short Answer)
4.8/5  (37)
(37)
What is the sum of the measures of the exterior angles, one at each vertex, of every convex polygon? Explain your reasoning.
(Essay)
4.8/5  (35)
(35)
State a fact that is true for all rhombi but not true for all kites.
(Short Answer)
4.9/5  (30)
(30)
Any fact that is true for every parallelogram is also true for every square.
(True/False)
4.8/5  (32)
(32)
Draw a tree diagram showing the hierarchy of the following quadrilaterals: kites, trapezoids, parallelograms, squares, rhombuses, isosceles trapezoids, and rectangles. (Note: Use "quadrilaterals" at the top of your diagram.)
(Essay)
4.8/5  (26)
(26)
When asked to find the sum of the interior angles in a hexagon, a student writes the statement alongside the sketch below. Comment on whether the student's mathematical reasoning is correct or incorrect. If it is correct, explain how you know. If it is incorrect, explain what was incorrect about the student's thinking and what he/she would have to do to correct the error. 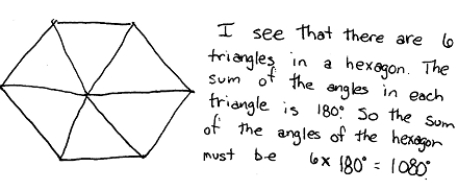
(Essay)
5.0/5  (29)
(29)
Showing 41 - 60 of 75
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)