Exam 14: Applications of Partial Derivatives
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
(i) Maximize 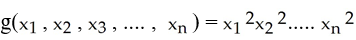 subject to the constraint x12 +x22 + ..... xn2 = 1.
(ii) Use part (i) to prove the well-known Arithmetic-Geometric Inequality :
For any positive real numbers y1 , y2 , ....... yn ,
subject to the constraint x12 +x22 + ..... xn2 = 1.
(ii) Use part (i) to prove the well-known Arithmetic-Geometric Inequality :
For any positive real numbers y1 , y2 , ....... yn ,
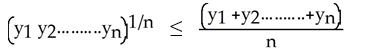
(Essay)
4.7/5  (41)
(41)
Find the maximum and minimum values of the function f(x, y, z) = 3x2 + 3y2 + 5 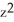 + 2xy - 2xz - 2yz over the sphere x2 + y2 + z2 = 6.
+ 2xy - 2xz - 2yz over the sphere x2 + y2 + z2 = 6.
(Multiple Choice)
4.9/5  (43)
(43)
Find the value of the constant a so that the graph of the function f(x) = ax2 best fits the curve y = ![Find the value of the constant a so that the graph of the function f(x) = ax<sup>2</sup> best fits the curve y = on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.](https://storage.examlex.com/TB9661/11ee77e1_77ae_917d_a0f8_133208b18574_TB9661_11.jpg) on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.
on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.
(Multiple Choice)
4.8/5  (28)
(28)
Use Newton's method to find a first quadrant solution of the system x2 + y4 = 1, y3 = 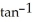 (
( 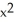 ).
).
(Multiple Choice)
4.9/5  (36)
(36)
Find the absolute maximum and absolute minimum values of f(x , y) = cos(x) + cos(y) - cos(x + y) - 1 on the closed square region bounded by the straight lines x = 0, y = 0, x = , and y = .
(Multiple Choice)
4.8/5  (35)
(35)
Find the absolute maximum and minimum values of f(x, y) = x2 - 3x + y2 - 3y + 5 on the triangle bounded by x = 0, y = 0, and x + y = 2.
(Multiple Choice)
4.7/5  (35)
(35)
Find the minimum value of the function f(x, y) = x4 + y4 - xy + xy2
(Multiple Choice)
4.9/5  (33)
(33)
Find an equation of the line of best fit given the following points: (1, -1), (2, 1), (3, 2), (4, 1), and (5, 0).
(Multiple Choice)
4.8/5  (31)
(31)
Find the absolute maximum and minimum values of f(x, y) = xy on the disk x2 + y2 1.
(Multiple Choice)
4.9/5  (38)
(38)
Find all critical points of f(x) = 2x3y -4x3 + 6y3 -18y + 19.
(Multiple Choice)
5.0/5  (32)
(32)
Find the maximum and minimum values of the function f(x, y) = 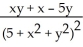 .
.
(Multiple Choice)
4.8/5  (26)
(26)
Find the maximum and minimum values of the function f(x, y, z, u, v) = x2 + y2 + z2 + u2 + v2 subject to the constraints x + y + 3z = 7 and 3z - u -v = 13.
(Multiple Choice)
4.9/5  (32)
(32)
A closed rectangular container of volume 96 cubic metres is to be made from three different materials.The top and the bottom of the container are to be made from a material that costs $4 per square metre, two parallel sides (say left and right) are to be made from a material that costs $3 per square metre, and the other two parallel sides (front and back) are to be made from a material that costs $1 per square metre.Let x and y be the dimensions of the base of the container and z be its height in metres.(i) Express the total cost of the container (in dollars) as a function of x and y.(ii) Find dimensions of the most economical container and how much it costs.
(Essay)
4.9/5  (36)
(36)
Find the envelope of the family of straight lines xcosh(c) + ysinh(c) = 3.
(Essay)
4.8/5  (28)
(28)
Use Lagrange multipliers to find the extreme values of f(x, y) = x2 + 3y2 + 2y on the unit circle x2 + y2 = 1.
(Multiple Choice)
4.7/5  (35)
(35)
Find the maximum and minimum values of f(x, y) = x2 + 3y2 + 2y on the disk x2 + y2 1. Use Lagrange multipliers to handle the boundary analysis.
(Multiple Choice)
4.8/5  (33)
(33)
Find and classify all critical points for the function f(x, y) = 2y3 + 3y2 - 12y -x2 + 2x.
(Multiple Choice)
4.9/5  (30)
(30)
Use Lagrange multipliers to find the maximum and minimum values of the functionf(x, y) = x2y + z subject to the constraints x2 + y2 = 1 and z = y.
(Multiple Choice)
4.8/5  (37)
(37)
Find and classify the critical points of f(x, y) = (2 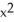 - xy + 5
- xy + 5 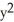 - x + 2y)
- x + 2y) 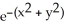 .
.
(Essay)
4.9/5  (38)
(38)
Showing 41 - 60 of 67
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)