Exam 14: Applications of Partial Derivatives
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Find the absolute maximum and minimum values of f(x, y) = 4(x - x2) sin( y) on the rectangle 0 x 1, 0 y 2 and the points where they are assumed.
(Multiple Choice)
4.7/5  (26)
(26)
Use Lagrange multipliers to find the maximum and minimum values of the functionf(x, y, z) = xy2z3 on the sphere x2 + y2 + z2 = 6.
(Multiple Choice)
4.8/5  (37)
(37)
Find the maximum and minimum distances from the origin to the ellipse 5x2 + 6xy + 5y2 - 8 = 0.
(Multiple Choice)
4.9/5  (25)
(25)
The extreme values of the function f(x , y, z) = 23 x + y2z subject to the constraintsx - z = 0 and y2 + z2 = 36 are given by:
(Multiple Choice)
4.8/5  (38)
(38)
Let pi > 0, i = 1, 2, 3,..., n be real numbers such that 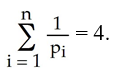 Find the maximum value of
Find the maximum value of 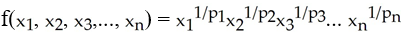 subject to the constraint
subject to the constraint 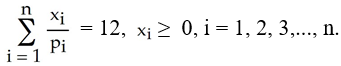
(Short Answer)
4.8/5  (36)
(36)
Find the point on the surface z = x2 + y2 closest to the point (1, 1, 0).
(Multiple Choice)
4.8/5  (39)
(39)
Suppose that a function f(x,y) has a critical point (a, b) at an interior point in its domain and that f has continuous second order partials in a neighbourhood of (a, b).
If 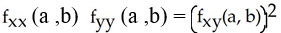 , then f has no local extremum at (a, b).
, then f has no local extremum at (a, b).
(True/False)
4.9/5  (35)
(35)
Find the point on the sphere x2 + y2 + z2 = 10 that is closest to the point (1, -8, 5).
(Multiple Choice)
4.7/5  (29)
(29)
Find the absolute maximum and minimum values of the linear function f(x, y) = -2x + y - 10 on the polygon 0 x 2, 0 y 2, y - x 1.
(Multiple Choice)
4.9/5  (44)
(44)
Use Maple's fsolve routine to solve the non-linear system of equations 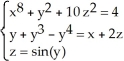 Quote the solution to 5 significant figures.
Quote the solution to 5 significant figures.
(Essay)
4.8/5  (38)
(38)
Let f(x, y, z) = x2 + 2y2 + 4z2. Find the point on the plane x + y + z = 14 at which f has its smallest value.
(Multiple Choice)
4.8/5  (36)
(36)
Find and classify the critical points of the Lagrange function L( 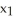 ,
, 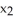 ,...,
,..., 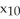 , λ) corresponding to the problem:extremize
, λ) corresponding to the problem:extremize 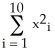 subject to =
subject to = 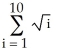 .
. 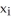
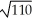
(Essay)
4.8/5  (45)
(45)
If a function f(x,y) has a local or absolute extreme value at the point (x0, y0) in its domain, then (x0, y0) must be either a critical point of f, a singular point of f, or a boundary point of the domain of f.
(True/False)
4.8/5  (38)
(38)
Find and classify all critical points for the function f(x, y) = x3 - 12xy2 + y3 + 45y.
(Multiple Choice)
4.7/5  (46)
(46)
Find the absolute maximum and minimum of f(x, y) = 4x2 + 2xy - 3y2 on the unit square0 x 1, 0 y 1.
(Multiple Choice)
4.9/5  (28)
(28)
Find and classify all critical points of f(x,y,z) = x3 + xz2 + 3x2 + y2 + 2z2 - 9x - 2y -10.
(Multiple Choice)
4.8/5  (27)
(27)
Find and classify the critical points of the following function: f(x, y) = 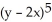 + 30x3 - 15y3.
+ 30x3 - 15y3.
(Multiple Choice)
4.9/5  (33)
(33)
If the Lagrange function L corresponding to the problem of extremizing f(x, y, z) subject to the constraint g(x, y, z) = 0 has exactly two critical points, then f must attain its maximum value at one of the points and attain its minimum value at the other point.
(True/False)
4.9/5  (28)
(28)
By first differentiating the integral, evaluate 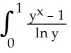 dy for x > -1.
dy for x > -1.
(Multiple Choice)
4.9/5  (37)
(37)
Showing 21 - 40 of 67
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)