Exam 7: Techniques of Integration
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Calculate the Trapezoid Rule approximations T2, T4, and T8 for I = 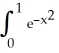 dx and use them to calculate the Simpson's Rule approximations S2, S4, and S8 and the Romberg approximations R1, R2, and R3 for I. Do all calculations to 9 decimal places. Then quote an approximate value for I to whatever precision you feel is justified by your calculations.
dx and use them to calculate the Simpson's Rule approximations S2, S4, and S8 and the Romberg approximations R1, R2, and R3 for I. Do all calculations to 9 decimal places. Then quote an approximate value for I to whatever precision you feel is justified by your calculations.
(Essay)
5.0/5  (31)
(31)
Use Simpson's Rule with 4 subintervals to approximate I = 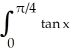 dx. Round your answer to 4 decimal places.
dx. Round your answer to 4 decimal places.
(Multiple Choice)
5.0/5  (42)
(42)
Let P(x) be a polynomial of degree 3, and suppose P(-2) = 1, P(0) = 3, and P(2) = 2.Find the exact value of 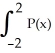 dx.
dx.
(Multiple Choice)
4.9/5  (37)
(37)
Evaluate the improper integral 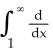
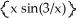 dx or show it diverges (to or - ).
dx or show it diverges (to or - ).
(Multiple Choice)
4.9/5  (33)
(33)
Use Simpson's Rule with 4 and 8 subintervals to approximate I = 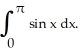 Give your answers to 5 decimal places. What are the actual errors in these approximations?
Give your answers to 5 decimal places. What are the actual errors in these approximations?
(Essay)
4.8/5  (37)
(37)
Evaluate the Trapezoid and Midpoint Rule approximations 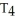 and
and 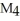 for
for 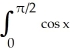 dx. Round your answer to 4 decimal places.
dx. Round your answer to 4 decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
Let f(x) be a function such that - 9 ![Let f(x) be a function such that - 9 \le (x) \le 3, for x [2, 4] and let J = dx. Find the maximum absolute error involved in approximating the integral J using the Trapezoid Rule T<sub>10</sub>.](https://storage.examlex.com/TB9661/11ee77e1_780a_93f5_a0f8_f7f4aa51fc60_TB9661_11.jpg) (x) 3, for x
(x) 3, for x![Let f(x) be a function such that - 9 \le (x) \le 3, for x [2, 4] and let J = dx. Find the maximum absolute error involved in approximating the integral J using the Trapezoid Rule T<sub>10</sub>.](https://storage.examlex.com/TB9661/11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11.jpg) [2, 4] and let J =
[2, 4] and let J = ![Let f(x) be a function such that - 9 \le (x) \le 3, for x [2, 4] and let J = dx. Find the maximum absolute error involved in approximating the integral J using the Trapezoid Rule T<sub>10</sub>.](https://storage.examlex.com/TB9661/11ee77e1_780a_93f6_a0f8_c117e5b071a6_TB9661_11.jpg) dx. Find the maximum absolute error involved in approximating the integral J using the Trapezoid Rule T10.
dx. Find the maximum absolute error involved in approximating the integral J using the Trapezoid Rule T10.
(Multiple Choice)
4.9/5  (36)
(36)
Suppose Trapezoid Rule and Midpoint Rule approximations T8 = 2.470 and M8 = 2.500 are known for the same integral I. Find the Simpson's Rule approximation S16 for I.
(Multiple Choice)
4.9/5  (33)
(33)
Showing 101 - 118 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)