Exam 7: Techniques of Integration
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Find the maximum value of ![Find the maximum value of on [0, 1], where f(x) = , and use it to obtain an upper bound for the absolute value of the error involved if the Trapezoid Rule approximation based on n equal subintervals is used to approximate I = dx. How large should n be chosen to ensure that the error does not exceed ?](https://storage.examlex.com/TB9661/11ee77e1_780a_93f7_a0f8_03dd5cc7102d_TB9661_11.jpg) on [0, 1], where f(x) =
on [0, 1], where f(x) = ![Find the maximum value of on [0, 1], where f(x) = , and use it to obtain an upper bound for the absolute value of the error involved if the Trapezoid Rule approximation based on n equal subintervals is used to approximate I = dx. How large should n be chosen to ensure that the error does not exceed ?](https://storage.examlex.com/TB9661/11ee77e1_780a_93f8_a0f8_5fc9fdeb6e8e_TB9661_11.jpg) , and use it to obtain an upper bound for the absolute value of the error involved if the Trapezoid Rule approximation based on n equal subintervals is used to approximate I =
, and use it to obtain an upper bound for the absolute value of the error involved if the Trapezoid Rule approximation based on n equal subintervals is used to approximate I = ![Find the maximum value of on [0, 1], where f(x) = , and use it to obtain an upper bound for the absolute value of the error involved if the Trapezoid Rule approximation based on n equal subintervals is used to approximate I = dx. How large should n be chosen to ensure that the error does not exceed ?](https://storage.examlex.com/TB9661/11ee77e1_780a_93f9_a0f8_0595bdc4a5e1_TB9661_11.jpg) dx. How large should n be chosen to ensure that the error does not exceed
dx. How large should n be chosen to ensure that the error does not exceed ![Find the maximum value of on [0, 1], where f(x) = , and use it to obtain an upper bound for the absolute value of the error involved if the Trapezoid Rule approximation based on n equal subintervals is used to approximate I = dx. How large should n be chosen to ensure that the error does not exceed ?](https://storage.examlex.com/TB9661/11ee77e1_780a_93fa_a0f8_0b5e0939252e_TB9661_11.jpg) ?
?
(Multiple Choice)
4.8/5  (39)
(39)
Suppose that 0 ![Suppose that 0 \le (x) \le 3 on the interval [0, 2] and that a Trapezoid Rule approximation T<sub>n</sub> for based on n equal subintervals of [0, 2] has been calculated. Which is the interval you can be sure must contain I?](https://storage.examlex.com/TB9661/11ee77e1_780a_45c3_a0f8_f1c8a9c032f1_TB9661_11.jpg) (x) 3 on the interval [0, 2] and that a Trapezoid Rule approximation Tn for
(x) 3 on the interval [0, 2] and that a Trapezoid Rule approximation Tn for ![Suppose that 0 \le (x) \le 3 on the interval [0, 2] and that a Trapezoid Rule approximation T<sub>n</sub> for based on n equal subintervals of [0, 2] has been calculated. Which is the interval you can be sure must contain I?](https://storage.examlex.com/TB9661/11ee77e1_780a_45c4_a0f8_c94503695902_TB9661_11.jpg) based on n equal subintervals of [0, 2] has been calculated. Which is the interval you can be sure must contain I?
based on n equal subintervals of [0, 2] has been calculated. Which is the interval you can be sure must contain I?
(Multiple Choice)
4.9/5  (41)
(41)
Evaluate the Midpoint Rule approximation 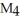 for
for 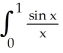 dx. Round your answer to 4 decimal places.
dx. Round your answer to 4 decimal places.
(Multiple Choice)
4.8/5  (40)
(40)
Suppose that the six subintervals Simpson's Rule and the three subintervals Midpoint Rule approximations for the integral 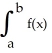 dx are respectively given by S6 = 42 and M3 =36.Determine the Trapezoid Rule approximation
dx are respectively given by S6 = 42 and M3 =36.Determine the Trapezoid Rule approximation 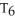 for the integral.
for the integral.
(Essay)
4.9/5  (29)
(29)
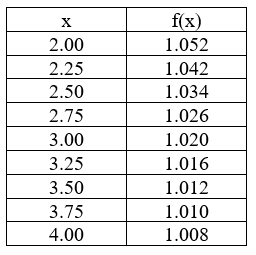
The following table gives values of an unknown function f(x) determined by experimental measurement. Find the best Midpoint Rule approximation you can for 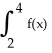 dx based on the values given in the table.
dx based on the values given in the table.
(Multiple Choice)
4.8/5  (40)
(40)
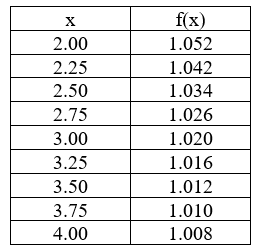
The following table gives values of an unknown function f(x) determined by experimental measurement. Find the best Trapezoid Rule approximation you can for 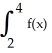 dx based on the values given in the table.
dx based on the values given in the table.
(Multiple Choice)
4.8/5  (46)
(46)
Evaluate the improper integral 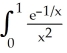 dx or show it to diverges (to or ).
dx or show it to diverges (to or ).
(Multiple Choice)
4.8/5  (32)
(32)
Showing 61 - 80 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)