Exam 7: Techniques of Integration
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Let G(x) = 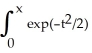 dt. Use Maple or another computer algebra system to calculate G(1) correct to 5 decimal places, and also to calculate
dt. Use Maple or another computer algebra system to calculate G(1) correct to 5 decimal places, and also to calculate 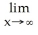 G(x).
G(x).
(Multiple Choice)
4.9/5  (40)
(40)
For what values of the constant k does the improper integral 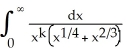 converge?
converge?
(Multiple Choice)
4.9/5  (35)
(35)
Find an upper bound for the size of the error if the Trapezoidal Rule using 4 equal subintervals is used to approximate the integral 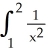 dx. Is the error positive or negative?
dx. Is the error positive or negative?
(Multiple Choice)
4.8/5  (40)
(40)
The integral I = 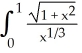 dx is improper and so unsuitable for numerical approximation by, say, the Trapezoid Rule or Simpson's Rule. Use a suitable change of variable to transform I into a proper integral these techniques can be applied to.
dx is improper and so unsuitable for numerical approximation by, say, the Trapezoid Rule or Simpson's Rule. Use a suitable change of variable to transform I into a proper integral these techniques can be applied to.
(Essay)
4.8/5  (40)
(40)
Find the Midpoint Rule approximation ![Find the Midpoint Rule approximation for I = based on dividing [0, 1] into 5 equal subintervals. Quote your answer to 4 decimal places. Calculate the exact value of I and so determine the error in the approximation.](https://storage.examlex.com/TB9661/11ee77e1_7809_d085_a0f8_cfdb59355d85_TB9661_11.jpg) for I =
for I = ![Find the Midpoint Rule approximation for I = based on dividing [0, 1] into 5 equal subintervals. Quote your answer to 4 decimal places. Calculate the exact value of I and so determine the error in the approximation.](https://storage.examlex.com/TB9661/11ee77e1_7809_d086_a0f8_f3d2ac96f4c4_TB9661_11.jpg) based on dividing [0, 1] into 5 equal subintervals. Quote your answer to 4 decimal places. Calculate the exact value of I and so determine the error in the approximation.
based on dividing [0, 1] into 5 equal subintervals. Quote your answer to 4 decimal places. Calculate the exact value of I and so determine the error in the approximation.
(Multiple Choice)
4.9/5  (36)
(36)
The values of a continuous function f on the closed interval [2, 20] are provided in the table below: ![The values of a continuous function f on the closed interval [2, 20] are provided in the table below: Use the table to find the Simpson's Rule approximation S<sub>6</sub> for dx.](https://storage.examlex.com/TB9661/11ee77e1_780d_7a64_a0f8_132605dc9bce_TB9661_00.jpg) Use the table to find the Simpson's Rule approximation S6 for
Use the table to find the Simpson's Rule approximation S6 for ![The values of a continuous function f on the closed interval [2, 20] are provided in the table below: Use the table to find the Simpson's Rule approximation S<sub>6</sub> for dx.](https://storage.examlex.com/TB9661/11ee77e1_780d_7a65_a0f8_53800a168ca9_TB9661_11.jpg) dx.
dx.
(Short Answer)
4.9/5  (30)
(30)
Evaluate the Trapezoid Rule approximation 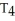 for
for 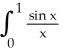 dx. Round your answer to 4 decimal places.
dx. Round your answer to 4 decimal places.
(Multiple Choice)
4.7/5  (42)
(42)
If g(x) is a polynomial of degree two, then the error involved in approximating the integral 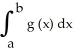 using the Trapezoid Rule
using the Trapezoid Rule 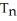 is zero.
is zero.
(True/False)
5.0/5  (38)
(38)
Determine the exact error involved in approximating the integral 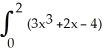 dx using the Simpson's Rule S20 .
dx using the Simpson's Rule S20 .
(Multiple Choice)
4.8/5  (30)
(30)
Use Simpson's Rule with 8 subintervals to approximate I = 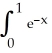 dx. Round your answer to 6 decimal places.
dx. Round your answer to 6 decimal places.
(Multiple Choice)
4.8/5  (34)
(34)
Let In = 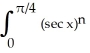 dx. Find a reduction formula for In in terms of In-2 valid for n 3and use it to evaluate I5 =
dx. Find a reduction formula for In in terms of In-2 valid for n 3and use it to evaluate I5 = 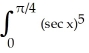 dx.
dx.
(Multiple Choice)
4.9/5  (44)
(44)
Showing 81 - 100 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)