Exam 2: Limits and Continuity
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Given f(x) = 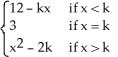 find the value of the constant real number k such that f is continuous at x = k.
find the value of the constant real number k such that f is continuous at x = k.
(Multiple Choice)
4.8/5  (44)
(44)
Use the formal definition of the limit to verify the addition property of limits: If ![Use the formal definition of the limit to verify the addition property of limits: If f(x) = L and g(x) = K, then [f(x) + g(x)] = L + K.](https://storage.examlex.com/TB9661/11ee77e1_785c_ab46_a0f8_4942268cd494_TB9661_11.jpg) f(x) = L and
f(x) = L and ![Use the formal definition of the limit to verify the addition property of limits: If f(x) = L and g(x) = K, then [f(x) + g(x)] = L + K.](https://storage.examlex.com/TB9661/11ee77e1_785c_ab47_a0f8_ad3218208f27_TB9661_11.jpg) g(x) = K, then
g(x) = K, then ![Use the formal definition of the limit to verify the addition property of limits: If f(x) = L and g(x) = K, then [f(x) + g(x)] = L + K.](https://storage.examlex.com/TB9661/11ee77e1_785c_ab48_a0f8_95417e74be09_TB9661_11.jpg) [f(x) + g(x)] = L + K.
[f(x) + g(x)] = L + K.
(Essay)
4.8/5  (30)
(30)
The temperature of an object at time t minutes is ![The temperature of an object at time t minutes is degrees. What is the rate of change of the temperature over the time interval [t, t + h]? How fast is the temperature changing at t = 1?](https://storage.examlex.com/TB9661/11ee77e1_7854_94e6_a0f8_61b9c7491faf_TB9661_11.jpg) degrees. What is the rate of change of the temperature over the time interval [t, t + h]? How fast is the temperature changing at t = 1?
degrees. What is the rate of change of the temperature over the time interval [t, t + h]? How fast is the temperature changing at t = 1?
(Multiple Choice)
4.9/5  (31)
(31)
Let f and g be continuous functions on the interval ( - , ) such that f has a zero on the closed interval I, and g has a zero on the closed interval.Which of the following functions must have at least one zero on the closed interval I ?
(Multiple Choice)
4.9/5  (25)
(25)
In which of the intervals (-2, -1), (-1, 0), (0, 1), and (1, 2) does the intermediate value theorem imply that f(x) = 2 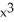 - 4
- 4 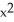 + 5x - 4 must have a zero?
+ 5x - 4 must have a zero?
(Multiple Choice)
4.8/5  (33)
(33)
If f(x) is a function defined on the closed interval [a , b] such that f(a) < 0 and f(b) > 0 , then the function f must have at least one zero in the interval [a , b].
(True/False)
4.9/5  (35)
(35)
Showing 21 - 40 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)