Exam 2: Limits and Continuity
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
An object moves along the x-axis so that its velocity at time t seconds is v(t) = ![An object moves along the x-axis so that its velocity at time t seconds is v(t) = m/s. What is the average acceleration (i.e., average rate of change of the velocity) of the object over the time interval[2, 2 + h]? What is the acceleration of the object at time t = 2s?](https://storage.examlex.com/TB9661/11ee77e1_7854_46b1_a0f8_81b2643dd7e6_TB9661_11.jpg) m/s. What is the average acceleration (i.e., average rate of change of the velocity) of the object over the time interval[2, 2 + h]? What is the acceleration of the object at time t = 2s?
m/s. What is the average acceleration (i.e., average rate of change of the velocity) of the object over the time interval[2, 2 + h]? What is the acceleration of the object at time t = 2s?
(Multiple Choice)
4.8/5  (37)
(37)
An object moves along the x-axis so that at time t seconds (where t 0) it is x = ![An object moves along the x-axis so that at time t seconds (where t \ge 0) it is x = m to the right of the origin. By calculating the average velocity of the object over time intervals [4, 4 + h] for h = 0.1, h = 0.01, h = 0.001, and h = 0.0001, determine the velocity of the particle at time t = 4s.](https://storage.examlex.com/TB9661/11ee77e1_7854_1fa0_a0f8_99cc2261d191_TB9661_11.jpg) m to the right of the origin. By calculating the average velocity of the object over time intervals [4, 4 + h] for h = 0.1, h = 0.01, h = 0.001, and h = 0.0001, determine the velocity of the particle at time t = 4s.
m to the right of the origin. By calculating the average velocity of the object over time intervals [4, 4 + h] for h = 0.1, h = 0.01, h = 0.001, and h = 0.0001, determine the velocity of the particle at time t = 4s.
(Multiple Choice)
4.9/5  (42)
(42)
Given f(x) = 4x + 7 and a number 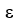 > 0, find the largest value of
> 0, find the largest value of 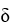 for which 0 <
for which 0 < 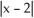 < 11ee7b11_3aa8_6932_ae82_3b68ee6209d9_TB9661_11 will imply that
< 11ee7b11_3aa8_6932_ae82_3b68ee6209d9_TB9661_11 will imply that 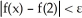 .
.
(Multiple Choice)
4.8/5  (35)
(35)
The polynomial function P(x) = ![The polynomial function P(x) = + - 7 - 2x + 10 has a zero in the closed interval [1 , 2].](https://storage.examlex.com/TB9661/11ee77e1_785a_8845_a0f8_d35ca87cb855_TB9661_11.jpg) +
+ ![The polynomial function P(x) = + - 7 - 2x + 10 has a zero in the closed interval [1 , 2].](https://storage.examlex.com/TB9661/11ee77e1_785a_8846_a0f8_55eb4a41d96f_TB9661_11.jpg) - 7
- 7 ![The polynomial function P(x) = + - 7 - 2x + 10 has a zero in the closed interval [1 , 2].](https://storage.examlex.com/TB9661/11ee77e1_785a_8847_a0f8_4fe5718537c5_TB9661_11.jpg) - 2x + 10 has a zero in the closed interval [1 , 2].
- 2x + 10 has a zero in the closed interval [1 , 2].
(True/False)
4.8/5  (37)
(37)
Complete the following definition: We say 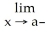 f(x) = L if for every
f(x) = L if for every 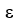 > 0 there exists
> 0 there exists 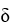 > 0 depending on 11ee7b11_3aa8_6932_ae82_3b68ee6209d9_TB9661_11 such that
> 0 depending on 11ee7b11_3aa8_6932_ae82_3b68ee6209d9_TB9661_11 such that
(Multiple Choice)
4.8/5  (36)
(36)
Showing 41 - 60 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)