Exam 7: Linear Programming
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Provide an appropriate response.
-Describe the feasible region of and .
(Multiple Choice)
4.9/5  (41)
(41)
Each day Larry needs at least 10 units of vitamin A, 12 units of vitamin B, and 20 units of vitamin C. Pill \#1 contains 4 units of and 3 of B. Pill \#2 contains 1 unit of A, 2 of B, and 4 of C. Pill \#3 contains 10 units of A, 1 of B, and 5 of .
-Pill #1 costs 2 cents, pill #2 costs 5 cents, and pill #3 costs 8 cents. Larry wants to minimize cost. What is the constraint inequality for vitamin ?
(Multiple Choice)
4.9/5  (27)
(27)
Introduce slack variables as necessary and write the initial simplex tableau for the problem.
-Maximize
Subject to:
3+5\leq74 \geq0,\geq0

(Multiple Choice)
4.9/5  (22)
(22)
Use the indicated entry as the pivot and perform the pivoting once.
-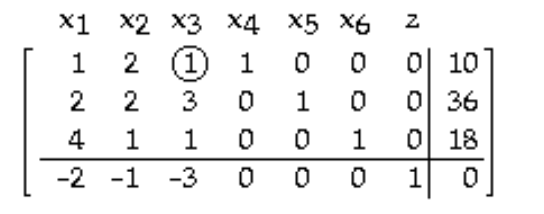
(Multiple Choice)
4.8/5  (34)
(34)
Convert the objective function into a maximization function.
-Minimize
Subject to:
(Multiple Choice)
4.8/5  (43)
(43)
A manufacturer of wooden chairs and tables must decide in advance how many of each item will be made in a givenweek. Use the table to find the system of inequalities that describes the manufacturer's weekly production.
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.
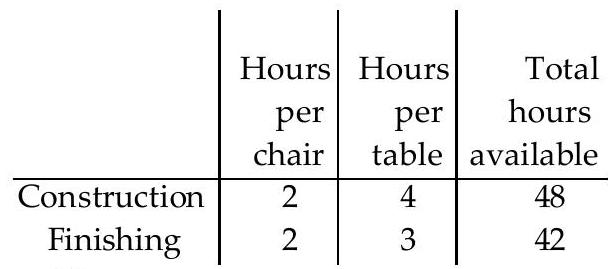
(Multiple Choice)
4.8/5  (42)
(42)
Provide an appropriate response.
-No unique optimum solution found from a simplex tableau corresponds to
(Short Answer)
4.9/5  (41)
(41)
Find the value(s) of the function on the given feasible region.
-Find the maximum and minimum of .
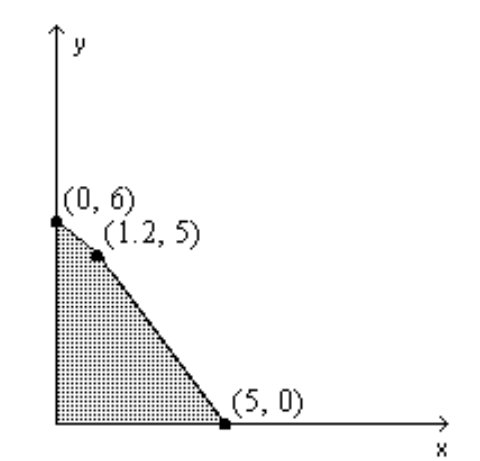
(Multiple Choice)
4.8/5  (26)
(26)
Write the word or phrase that best completes each statement or answers thequestion.
-Explain how you decide which half-plane to shade when you are graphing an inequality.
(Essay)
4.8/5  (42)
(42)
Provide an appropriate response.
-If the inequalities and are included in a system, the feasibility region is restricted to the axes and which quadrant?
(Multiple Choice)
4.8/5  (29)
(29)
A manufacturing company wants to maximize profits on products , and . The profit margin is for for , and for . The production requirements and departmental capacities are as follows:
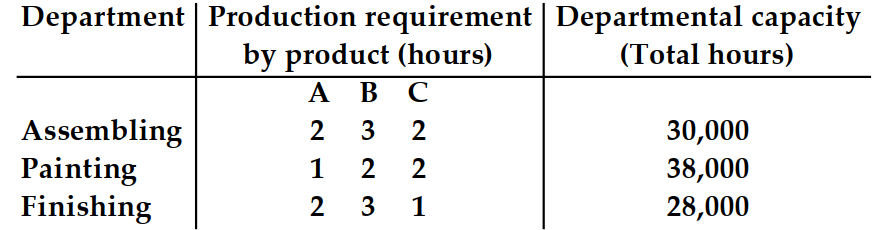 -What is the constraint for the assembling department?
-What is the constraint for the assembling department?
(Multiple Choice)
4.8/5  (42)
(42)
Write the word or phrase that best completes each statement or answers thequestion.
-Explain why the solution to a linear programming problem always occurs at a corner point of the feasible region.
(Essay)
4.8/5  (29)
(29)
Provide an appropriate response.
-A linear program is defined with constraints , and . Is the feasibility region bounded, unbounded, or empty?
(Multiple Choice)
4.7/5  (33)
(33)
Write the basic solution for the simplex tableau determined by setting the nonbasic variables equal to 0.
-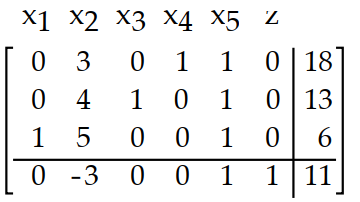
(Multiple Choice)
4.9/5  (39)
(39)
Use the simplex method to solve the linear programming problem.
-Maximize
Subject to:
With
(Multiple Choice)
4.8/5  (46)
(46)
Use the two-stage method to solve.
-Find such that
+3+2\leq60 +2+3\geq36
And is maximized.
(Multiple Choice)
4.9/5  (44)
(44)
Showing 21 - 40 of 203
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)