Exam 7: Linear Programming
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Solve the problem.
-The manager of a concert hall estimates that 600 people attend each classical concert, that 1000 people attend each jazz concert, and that 300 people attend each rock concert. In any given month, the total of the number of classical concerts and the number of jazz concerts may not exceed 9 and the number of rock concerts must be no more than 8 . Furthermore there should be twice as many rock concerts as classical concerts in any given month. How many of each type of concert should there be in a month to maximize attendance?
(Multiple Choice)
4.9/5  (40)
(40)
A toy making company has at least 300 squares of felt, of stuffing, and of trim to make dogs and dinosaurs.
A dog uses 1 square of felt, of stuffing, and of trim. A dinosaur uses 2 squares of felt, of stuffing, and of trim.
-It costs the company to make each dog and for each dinosaur. The company wants to minimize its costs. What are the constants in the corresponding dual model?
(Multiple Choice)
4.9/5  (26)
(26)
Use graphical methods to solve the linear programming problem.
-Minimize
Subject to:
(Multiple Choice)
4.9/5  (35)
(35)
Each day Larry needs at least 10 units of vitamin A, 12 units of vitamin B, and 20 units of vitamin C. Pill \#1 contains 4 units of and 3 of B. Pill \#2 contains 1 unit of A, 2 of B, and 4 of C. Pill \#3 contains 10 units of A, 1 of B, and 5 of .
-Pill #1 costs 8 cents, pill #2 costs 11 cents, and pill #3 costs 6 cents. Larry wants to minimize cost. What are the constants in the problem?
(Multiple Choice)
4.9/5  (29)
(29)
Convert the constraints into linear equations by using slack variables.
-Maximize
Subject to:
(Multiple Choice)
4.8/5  (35)
(35)
A manufacturer of wooden chairs and tables must decide in advance how many of each item will be made in a givenweek. Use the table to find the system of inequalities that describes the manufacturer's weekly production.
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.
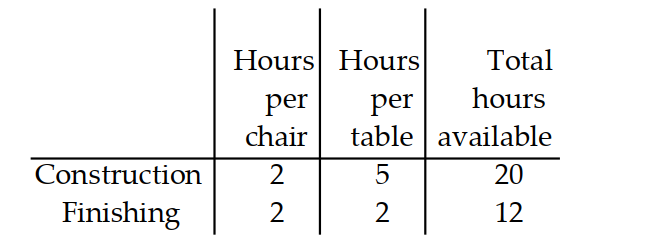
(Multiple Choice)
4.8/5  (32)
(32)
Rewrite the system of inequalities, adding slack variables or subtracting surplus variables as needed.
-
(Multiple Choice)
4.8/5  (33)
(33)
Use graphical methods to solve the linear programming problem.
-Maximize
Subject to:
(Multiple Choice)
4.8/5  (33)
(33)
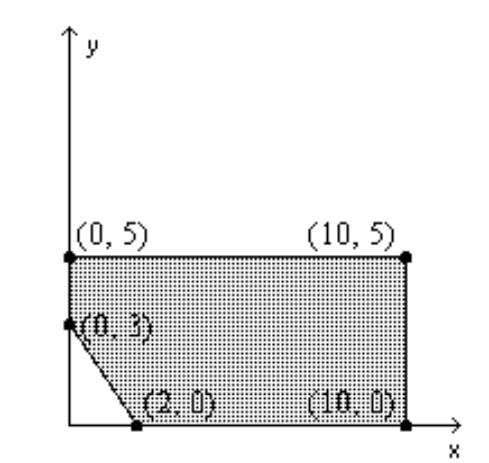
Find the value(s) of the function on the given feasible region.
-Find the maximum and minimum of .
(Multiple Choice)
4.8/5  (30)
(30)
Graph the feasible region for the system of inequalities.
-
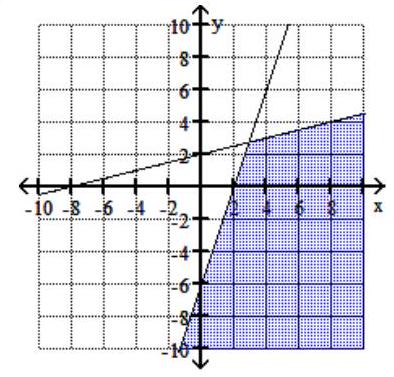
(Multiple Choice)
5.0/5  (33)
(33)
Use the simplex method to solve the linear programming problem.
-Maximize
Subject to:
With
(Multiple Choice)
4.8/5  (37)
(37)
The Acme Class Ring Company designs and sells two types of rings: the VIP and the SST. They can produce up to 24rings each day using up to 60 total man hours of labor. It takes 3 man hours to make one VIP ring, versus 2 man hoursto make one SST ring.
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
(Multiple Choice)
4.7/5  (36)
(36)
Introduce slack variables as necessary and write the initial simplex tableau for the problem.
-Maximize
Subject to:

(Multiple Choice)
4.7/5  (34)
(34)
Solve the problem.
-A toy manufacturer makes three types of toys. Toy A requires 12 minutes to assemble, 12 minutes to paint, 4 minutes to package, and sells for . Toy B requires 20 minutes to assemble, 12 minutes to paint, 8 minutes to package, and sells for . Toy requires 24 minutes to assemble, 20 minutes to paint, 16 minutes to package, and sells for . The manufacturer has available 800 work-minutes for assembly, 600 work-minutes for painting, and 720 work-minutes for packaging each day. They must make at least 10 toys of type A and 15 of type each day. How many of each type of toy should be produced each day to maximize revenues?
(Multiple Choice)
4.8/5  (33)
(33)
Provide an appropriate response.
-Does a linear program with at least three constraints always have a closed feasible region?
(True/False)
4.9/5  (32)
(32)
Showing 81 - 100 of 203
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)