Exam 7: Linear Programming
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Solve the problem.
-An athlete uses three different exercise regimens for increasing cardiovascular fitness. An hour of regimen A rates a 3 in effectiveness, an hour of regimen rates a 4 in effectiveness, and an hour of regimen rates a 5 in effectiveness. In any given week, the athlete can train at most 5 hours by regimen . In any given week the combined hours of regimens and may not exceed 9. In any given week the combined hours of regimens B and C may not exceed 10. How many hours of each regimen should the athlete perform in a week in order to maximize the increase in fitness?
(Multiple Choice)
5.0/5  (32)
(32)
Use the simplex method to solve the linear programming problem.
-Maximize
Subject to:
With
(Multiple Choice)
4.7/5  (45)
(45)
Graph the feasible region for the system of inequalities.
-
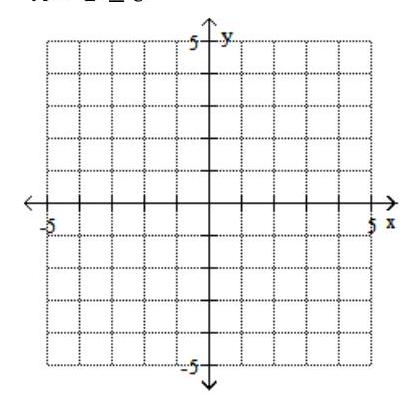
(Multiple Choice)
4.9/5  (33)
(33)
Graph the feasible region for the system of inequalities.
-
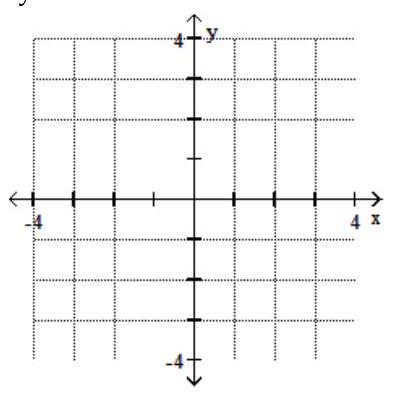
(Multiple Choice)
4.9/5  (39)
(39)
A manufacturing company wants to maximize profits on products , and . The profit margin is for for , and for . The production requirements and departmental capacities are as follows:
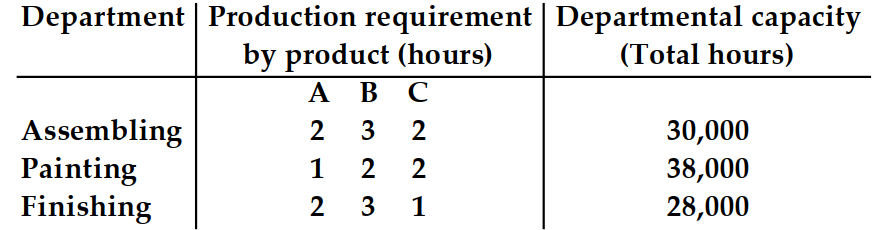 -What is the constraint for the finishing department?
-What is the constraint for the finishing department?
(Multiple Choice)
4.9/5  (34)
(34)
Write the word or phrase that best completes each statement or answers thequestion.
-Explain why the graphing method is not satisfactory for solving a linear programming problem with 3 variables.
(Essay)
4.9/5  (35)
(35)
Find the value(s) of the function, subject to the system of inequalities.
-Find the minimum of subject to:
.
(Multiple Choice)
4.9/5  (45)
(45)
Graph the feasible region for the system of inequalities.
-
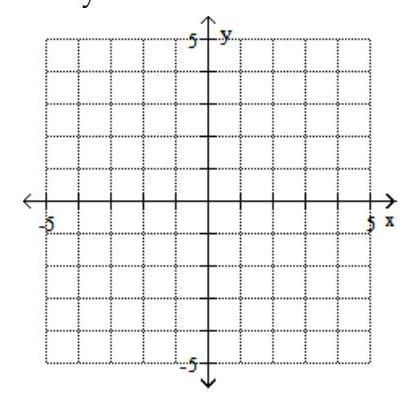
(Multiple Choice)
5.0/5  (25)
(25)
Provide an appropriate response.
-The feasible region of a set of two inequalities must always be unbounded.
(True/False)
4.8/5  (34)
(34)
Convert the constraints into linear equations by using slack variables.
-Maximize
Subject to:
+6+\leq24 \geq0,\geq0,\geq0
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-An electronics store stocks VCRs, stereo systems, and television sets. They have limited storage space and can stock a total of at most 80 of these three machines. They know from past experience that they should stock twice as many VCRs as stereo systems and at least 20 television sets. If each VCR sells for , each stereo system sells for , and each television set sells for , how many of each should be stocked and sold for maximum revenues?
(Multiple Choice)
4.9/5  (30)
(30)
Write the basic solution for the simplex tableau determined by setting the nonbasic variables equal to 0.
-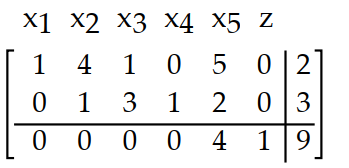
(Multiple Choice)
4.9/5  (31)
(31)
Graph the feasible region for the system of inequalities.
-
(Multiple Choice)
4.8/5  (34)
(34)
State the dual problem. Use , and as the variables. Given: , and .
-Minimize
Subject to:
(Multiple Choice)
5.0/5  (30)
(30)
Provide an appropriate response.
-Is it possible that the feasible region of a linear program include more than one distinct area?
(True/False)
4.8/5  (39)
(39)
Convert the constraints into linear equations by using slack variables.
-Maximize
Subject to:
(Multiple Choice)
4.8/5  (42)
(42)
Write the basic solution for the simplex tableau determined by setting the nonbasic variables equal to 0.
-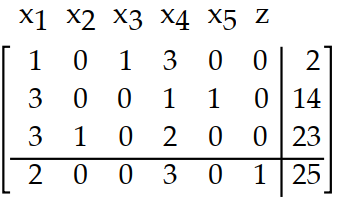
(Multiple Choice)
4.9/5  (27)
(27)
Convert the objective function into a maximization function.
-Minimize
Subject to:
(Multiple Choice)
5.0/5  (26)
(26)
Showing 161 - 180 of 203
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)