Exam 7: Linear Programming
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Introduce slack variables as necessary and write the initial simplex tableau for the problem.
-Maximize
Subject to:

(Multiple Choice)
4.8/5  (30)
(30)
A toy making company has at least 300 squares of felt, of stuffing, and of trim to make dogs and dinosaurs.
A dog uses 1 square of felt, of stuffing, and of trim. A dinosaur uses 2 squares of felt, of stuffing, and of trim.
-It costs the company to make each dog and for each dinosaur. What is the company's minimum cost?
(Multiple Choice)
4.9/5  (35)
(35)
Use the two-stage method to solve.
- Minimize w=18+11 subject to: 2+2=14 6+2\geq36 2+4\leq24 \geq0,\geq0
(Multiple Choice)
4.8/5  (36)
(36)
The Acme Class Ring Company designs and sells two types of rings: the VIP and the SST. They can produce up to 24rings each day using up to 60 total man hours of labor. It takes 3 man hours to make one VIP ring, versus 2 man hoursto make one SST ring.
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
(Multiple Choice)
4.9/5  (32)
(32)
Provide an appropriate response.
-Consider a linear program with an objective function for profit. Thinking of isoprofit lines, if the objective function is evaluated at the corner points of polygon , and , and , is it safe to assume that is not the corner point at which the profit is maximized?
(True/False)
4.8/5  (46)
(46)
Use the two-stage method to solve.
-Find and such that
+\leq25 +2\geq15 2+\leq30
And is maximized.
(Multiple Choice)
4.9/5  (37)
(37)
Write the basic solution for the simplex tableau determined by setting the nonbasic variables equal to 0.
-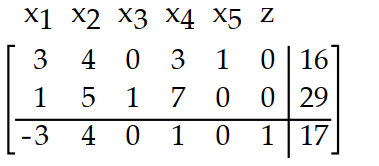
(Multiple Choice)
4.8/5  (25)
(25)
A bakery makes sweet rolls and donuts. A batch of sweet rolls requires of flour, 1 dozen eggs, and of sugar. Abatch of donuts requires of flour, 3 dozen eggs, and of sugar. Set up an initial simplex tableau to maximizeprofit.
-The bakery has of flour, 260 dozen eggs, of sugar. The profit on a batch of sweet rolls is and on a batch of donuts is .

(Multiple Choice)
4.8/5  (33)
(33)
Find the value(s) of the function on the given feasible region.
-Find the maximum and minimum of .
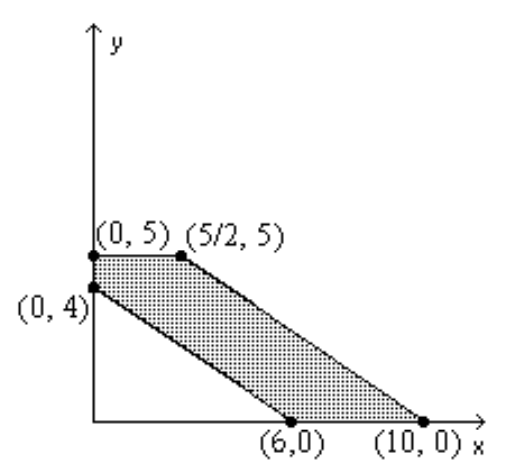
(Multiple Choice)
4.8/5  (36)
(36)
Each day Larry needs at least 10 units of vitamin A, 12 units of vitamin B, and 20 units of vitamin C. Pill \#1 contains 4 units of and 3 of B. Pill \#2 contains 1 unit of A, 2 of B, and 4 of C. Pill \#3 contains 10 units of A, 1 of B, and 5 of .
-Pill #1 costs 4 cents, pill #2 costs 5 cents, and pill #3 costs 8 cents. Larry wants to minimize cost. What is the constraint inequality for vitamin A?
(Multiple Choice)
4.8/5  (29)
(29)
Use the simplex method to solve the linear programming problem.
-Maximize
Subject to:
With
(Multiple Choice)
5.0/5  (35)
(35)
A manufacturer of wooden chairs and tables must decide in advance how many of each item will be made in a givenweek. Use the table to find the system of inequalities that describes the manufacturer's weekly production.
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.
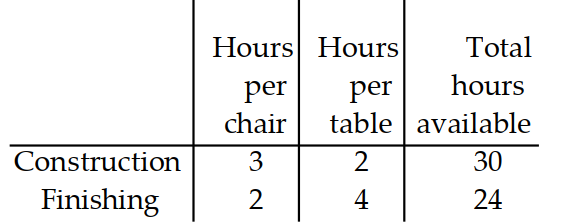
(Multiple Choice)
4.9/5  (28)
(28)
Find the value(s) of the function, subject to the system of inequalities.
-Find the maximum and minimum of subject to:
.
(Multiple Choice)
4.9/5  (36)
(36)
Use graphical methods to solve the linear programming problem.
-Maximize
Subject to:
(Multiple Choice)
4.8/5  (27)
(27)
Rewrite the system of inequalities, adding slack variables or subtracting surplus variables as needed.
-
(Multiple Choice)
4.9/5  (35)
(35)
Introduce slack variables as necessary and write the initial simplex tableau for the problem.
-Maximize
Subject to:

(Multiple Choice)
4.7/5  (34)
(34)
Showing 61 - 80 of 203
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)