Exam 13: Additional Topics in Regression Analysis

If ε_t is the error in time t,ε_t-1 is the error in the previous time period,ρ is the correlation coefficient,and μ_t a random variable with autocorrelation,which of the following is the first-order autoregressive model of autocorrelated behavior?

If dummy variables are used to represent distinct subsets or regions,then a linear relationship between predictor variables will result,and estimation of coefficients will be impossible.

A regression model with three independent variables was constructed to analyze certain data: y = β₀ + β₁X₁ + β₃X₃ + β₂X₂ + ε.But while estimating the coefficient,the following regression model was mistakenly used: y = α₀ + α₁x₁ + μ.From the second formula,which of the following can be deduced to be affecting the regression model?

What strategies can be employed to detect multicollinearity?

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: You are interested in examining the factors that determine the average length of stay in a hospital across states.You collect data on the following variables: Y = statewide average hospital stay X₁ = median state income X₂ = 1 if the state is in the Northeast,0 otherwise X₃ = 1 if the state is in the South,0 otherwise X₄ = 1 if the state is in the Midwest,0 otherwise X₅ = 1 if the state is in the West,0 otherwise -You run the following regression: Y = β₀ + β₁X₁ + β₂X₂ + β₃X₃ + β₄X₄.What effect does being a state in the West have on the average length of hospital stay?

When does multicollinearity occur in a multiple regression model?

If the Durbin-Watson statistic d has values greater than 4 - d_L,this indicates:

Dummy variables cannot be used to estimate the seasonal effects on a regression model applied to time-series data.

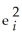THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: Suppose that a regression was run with two independent variables and 25 observations.The Durbin-Watson statistic was 2.28. -Consider a regression model that uses 50 observations.Let e_i denote the residuals from the fitted regression and _i the in-sample predicted values of the dependent variables.The least squares regression of on _i has coefficient of determination 0.028.What can you conclude from this finding?

You are interested in examining the factors that influence the amount of stock a person owns.As explanatory variables,you include both the person's income and also the amount of equity they have in their house.Which of the following problems would most likely affect your model?

If an analyst is regressing individual independent variables on all other independent variables of a regression model,he or she is testing for:

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: An economist is in the process of developing a model to predict the price of gold.She believes that the two most important variables are the price of a barrel of oil (x₁)and the interest rate (x₂).She proposes the model y = β₀ + β₁x₁ + β₂x₂ + β₃x₁x₃ + ε.A random sample of 20 daily observations was taken.The computer output is shown below. THE REGRESSION EQUATION IS y = 115.6 + 22.3x₁ + 14.7x₂ - 1.36x₁x₂ 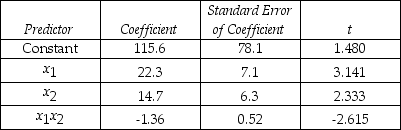S = 20.9 R-Sq = 55.4% ANALYSIS OF VARIANCE -Suppose that a regression relationship is given by Y = β₀ + β₁X₁ + β₂X₂ + ε.If the simple linear regression of Y on X₁ is estimated from a sample of n observations,the resulting slope estimate will generally be biased for β₁.But if the sample correlation between X₁ and X₂ is 0,the slope will not be biased for β₁. How does X₂ affect β₁ if the sample correlation between X₁ and X₂ is zero?

Consider the first-order model = 50 - 10x₁ + 8x₂ - 2x₁x₂.A 1-unit increase in x₁,while holding x₂ constant at a value of 4,decreases the value of y,on average,by:

Suppose you are interested in modeling the amount of money a household spends for a house.We would expect income to be a determining factor.In addition,the income tax rate for a household might be important since there are tax advantages to home ownership.If you were to run a regression of home purchase price on income and marginal tax rate,your results might be subject to:

Explain what is meant by multicollinearity.What effects does multicollinearity have on the results of regression coefficients?

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: Consider the following model: Y = β₀ + β₁X_1t + β₂X_2t + γ₃Y_t-1.Using a sample of 36 months,we estimate this model and obtain the following results: y_t = 1.33 + 17.6x_1t + 0.94x_2t + 0.39Y_t-1 -If X₁ were to increase by 1-unit in time t,by how much would we expect Y to change in period t?

When is a dummy variable used as an independent variable in a regression model?

Suppose we estimate the regression Y_t = β₀ + β₁X_1t + β₂X_2t + β₃X_3t + β₄X_4t + ε_t using 36 months of data.Using the residuals from this regression,we run another regression of 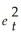on the predicted values _t.From this regression we get a coefficient of determination R² of 0.09.Let H₀ be that there is no heteroscedasticity.What can you conclude?

Why is it so important to understand and test the assumptions of the multiple regression model?

If the independent variables in a regression model are perfectly correlated,it will be impossible to estimate the regression coefficients.