Exam 17: Multiple Regression

From the coefficient of determination,we cannot detect the strength of the relationship between the dependent variable y and any individual independent variable.

If the value of the Durbin-Watson statistic d is large (d > 2),this indicates a(n)____________________ (positive/negative)first-order autocorrelation exists.

One of the consequences of multicollinearity in multiple regression is biased estimates on the slope coefficients.

A multiple regression equation has a coefficient of determination of 0.81.Then,the percentage of the variation in y that is explained by the regression equation is 90%.

Life Expectancy An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x₁),the cholesterol level (x₂),and the number of points that the individual's blood pressure exceeded the recommended value (x₃).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x₁− 0.021x₂− 0.061x₃ ​ S = 9.47 ​ R−Sq = 22.5% ANALYSIS OF VARIANCE ​ ​ -{Life Expectancy Narrative} Is there sufficient evidence at the 5% significance level to infer that the number of points that the individual's blood pressure exceeded the recommended value and the age at death are negatively linearly related?

In order to test the significance of a multiple regression model involving 4 independent variables and 25 observations,the numerator and denominator degrees of freedom for the critical value of F are 3 and 21,respectively.

Real Estate Builder A real estate builder wishes to determine how house size is influenced by family income,family size,and education of the head of household.House size is measured in hundreds of square feet,income is measured in thousands of dollars,and education is measured in years.A partial computer output is shown below. SUMMARY OUTPUT Regression Statistics Multiple R 0.865 R Square 0.748 Adjusted R Square 0.726 Standard Error 5.195 Observations 50 ANOVA ​ ​ -{Real Estate Builder Narrative} What minimum annual income would an individual with a family size of 4 and 16 years of education need to attain a predicted 10,000 square foot home?

Multicollinearity is present when there is a high degree of correlation between the independent variables included in the regression model.

Life Expectancy An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x₁),the cholesterol level (x₂),and the number of points that the individual's blood pressure exceeded the recommended value (x₃).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x₁− 0.021x₂− 0.061x₃ ​ S = 9.47 ​ R−Sq = 22.5% ANALYSIS OF VARIANCE ​ ​ -{Life Expectancy Narrative} Is there enough evidence at the 5% significance level to infer that the cholesterol level and the age at death are negatively linearly related?

One of the consequences of multicollinearity in multiple regression is inflated standard errors in some or all of the estimated slope coefficients.

For a multiple regression model,the total variation in y can be expressed as:

Real Estate Builder A real estate builder wishes to determine how house size is influenced by family income,family size,and education of the head of household.House size is measured in hundreds of square feet,income is measured in thousands of dollars,and education is measured in years.A partial computer output is shown below. SUMMARY OUTPUT Regression Statistics Multiple R 0.865 R Square 0.748 Adjusted R Square 0.726 Standard Error 5.195 Observations 50 ANOVA ​ ​ -{Real Estate Builder Narrative} When the builder used a simple linear regression model with house size as the dependent variable and education as the independent variable,he obtained an R-square value of 23.0%.What additional percentage of the total variation in house size has been explained by including family size and income in the multiple regression?

When there is more than one independent variable in a regression model,we refer to the graphical depiction of the equation as a(n)____________________ rather than as a straight line.

Real Estate Builder A real estate builder wishes to determine how house size is influenced by family income,family size,and education of the head of household.House size is measured in hundreds of square feet,income is measured in thousands of dollars,and education is measured in years.A partial computer output is shown below. SUMMARY OUTPUT Regression Statistics Multiple R 0.865 R Square 0.748 Adjusted R Square 0.726 Standard Error 5.195 Observations 50 ANOVA ​ ​ -{Real Estate Builder Narrative} Interpret the value of the Adjusted R-Square.

Student's Final Grade A statistics professor investigated some of the factors that affect an individual student's final grade in her course.She proposed the multiple regression model 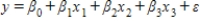,where y is the final grade (out of 100 points),x₁ is the number of lectures skipped,x₂ is the number of late assignments,and x₃ is the midterm exam score (out of 100).The professor recorded the data for 50 randomly selected students.The computer output is shown below. THE REGRESSION EQUATION IS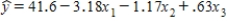 ​ ​ ​ S = 13.74 R−Sq = 30.0% ​ ANALYSIS OF VARIANCE ​ ​ -{Student's Final Grade Narrative} Does this data provide enough evidence to conclude at the 5% significance level that the model is useful in predicting the final grade?

The range of the values of the Durbin-Watson statistic d is:

Real Estate Builder A real estate builder wishes to determine how house size is influenced by family income,family size,and education of the head of household.House size is measured in hundreds of square feet,income is measured in thousands of dollars,and education is measured in years.A partial computer output is shown below. SUMMARY OUTPUT Regression Statistics Multiple R 0.865 R Square 0.748 Adjusted R Square 0.726 Standard Error 5.195 Observations 50 ANOVA ​ ​ -{Real Estate Builder Narrative} At the 0.01 level of significance,what conclusion should the builder draw regarding the inclusion of income in the regression model?

Real Estate Builder A real estate builder wishes to determine how house size is influenced by family income,family size,and education of the head of household.House size is measured in hundreds of square feet,income is measured in thousands of dollars,and education is measured in years.A partial computer output is shown below. SUMMARY OUTPUT Regression Statistics Multiple R 0.865 R Square 0.748 Adjusted R Square 0.726 Standard Error 5.195 Observations 50 ANOVA ​ ​ -{Real Estate Builder Narrative} What is the predicted house size for an individual earning an annual income of $40,000,having a family size of 4,and having 13 years of education?

Student's Final Grade A statistics professor investigated some of the factors that affect an individual student's final grade in her course.She proposed the multiple regression model 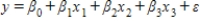,where y is the final grade (out of 100 points),x₁ is the number of lectures skipped,x₂ is the number of late assignments,and x₃ is the midterm exam score (out of 100).The professor recorded the data for 50 randomly selected students.The computer output is shown below. THE REGRESSION EQUATION IS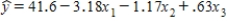 ​ ​ ​ S = 13.74 R−Sq = 30.0% ​ ANALYSIS OF VARIANCE ​ ​ -{Student's Final Grade Narrative} Interpret the coefficient b₂.

The parameter estimates are biased when multicollinearity is present in a multiple regression equation.