Exam 13: Experimental Design and Analysis of Variance
Exam 1: Data and Statistics85 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays112 Questions
Exam 3: Descriptive Statistics: Numerical Measures139 Questions
Exam 4: Introduction to Probability129 Questions
Exam 5: Discrete Probability Distributions150 Questions
Exam 6: Continuous Probability Distributions144 Questions
Exam 7: Sampling and Sampling Distributions119 Questions
Exam 8: Interval Estimation118 Questions
Exam 9: Hypothesis Tests118 Questions
Exam 10: Inference About Means and Proportions With Two Populations127 Questions
Exam 11: Inferences About Population Variances113 Questions
Exam 12: Tests of Goodness of Fit, Independence and Multiple Proportions76 Questions
Exam 13: Experimental Design and Analysis of Variance125 Questions
Exam 14: Simple Linear Regression103 Questions
Exam 15: Multiple Regression109 Questions
Exam 16: Regression Analysis: Model Building82 Questions
Exam 17: Time Series Analysis and Forecasting80 Questions
Exam 18: Nonparametric Methods83 Questions
Exam 19: Statistical Methods for Quality Control75 Questions
Exam 20: Decision Analysis71 Questions
Exam 21: Sample Survey68 Questions
Select questions type
Exhibit 13-4
In a completely randomized experimental design involving five treatments, thirteen observations were recorded for each of the five treatments. The following information is provided.SSTR = 200 (Sum Square Between Treatments)
SST = 800 (Total Sum Square)
-Refer to Exhibit 13-4. The conclusion of the test is that the five means
(Multiple Choice)
4.8/5  (39)
(39)
Random samples of employees from three different departments of MNM Corporation showed the following yearly incomes (in $1,000).  At = .05, test to determine if there is a significant difference among the average incomes of the employees from the three departments.
At = .05, test to determine if there is a significant difference among the average incomes of the employees from the three departments.
(Essay)
4.8/5  (44)
(44)
Exhibit 13-6
Part of an ANOVA table is shown below.  -Refer to Exhibit 13-6. The number of degrees of freedom corresponding to between treatments is
-Refer to Exhibit 13-6. The number of degrees of freedom corresponding to between treatments is
(Multiple Choice)
4.7/5  (36)
(36)
The critical F value with 6 numerator and 60 denominator degrees of freedom at = .05 is
(Multiple Choice)
4.7/5  (37)
(37)
In a completely randomized experimental design, 11 experimental units were used for each of the 4 treatments. Part of the ANOVA table is shown below.  Fill in the blanks in the above ANOVA table.
Fill in the blanks in the above ANOVA table.
(Essay)
4.8/5  (39)
(39)
Exhibit 13-3
To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below.  -Refer to Exhibit 13-3. The null hypothesis
-Refer to Exhibit 13-3. The null hypothesis
(Multiple Choice)
4.9/5  (31)
(31)
Exhibit 13-7
The following is part of an ANOVA table, which was the results of three treatments and a total of 15 observations.  -In testing for the equality of k population means, the number of treatments is
-In testing for the equality of k population means, the number of treatments is
(Multiple Choice)
5.0/5  (40)
(40)
Halls, Inc. has three stores located in three different areas. Random samples of the sales of the three stores (In $1,000) are shown below.  At a 5% level of significance, use Excel to test to see if there is a significant difference in the average sales of the three stores.
At a 5% level of significance, use Excel to test to see if there is a significant difference in the average sales of the three stores.
(Essay)
4.9/5  (35)
(35)
Exhibit 13-6
Part of an ANOVA table is shown below.  -Refer to Exhibit 13-6. The conclusion of the test is that the means
-Refer to Exhibit 13-6. The conclusion of the test is that the means
(Multiple Choice)
4.9/5  (32)
(32)
MNM, Inc. has three stores located in three different areas. Random samples of the daily sales of the three stores (in $1,000) are shown below.  At a 5% level of significance, test to see if there is a significant difference in the average sales of the three stores.
At a 5% level of significance, test to see if there is a significant difference in the average sales of the three stores.
(Essay)
4.7/5  (38)
(38)
Exhibit 13-1 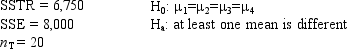 -Refer to Exhibit 13-1. The null hypothesis is to be tested at the 5% level of significance. The critical value from the table is
-Refer to Exhibit 13-1. The null hypothesis is to be tested at the 5% level of significance. The critical value from the table is
(Multiple Choice)
4.8/5  (49)
(49)
A research organization wishes to determine whether four brands of batteries for transistor radios perform equally well. Three batteries of each type were randomly selected and installed in the three test radios. The number of hours of use for each battery is given below.  Consider the three different test radios and use Excel to carry out the analysis of variance procedure for a randomized block design. Use a .05 level of significance.
Consider the three different test radios and use Excel to carry out the analysis of variance procedure for a randomized block design. Use a .05 level of significance.
(Essay)
4.8/5  (36)
(36)
The marketing department of a company has designed three different boxes for its product. It wants to determine which box will produce the largest amount of sales. Each box will be test marketed in five different stores for a period of a month. Below you are given the information on sales.  a.State the null and alternative hypotheses.
b.Construct an ANOVA table.
c.What conclusion do you draw?
d.Use Fisher's LSD procedure and determine which mean (if any) is different from the others. Let = 0.01.
a.State the null and alternative hypotheses.
b.Construct an ANOVA table.
c.What conclusion do you draw?
d.Use Fisher's LSD procedure and determine which mean (if any) is different from the others. Let = 0.01.
(Essay)
4.9/5  (42)
(42)
An experimental design that permits statistical conclusions about two or more factors is a
(Multiple Choice)
4.8/5  (42)
(42)
Halls, Inc. has three stores located in three different areas. Random samples of the sales of the three stores (In $1,000) are shown below.  At a 5% level of significance, test to see if there is a significant difference in the average sales of the three stores.
At a 5% level of significance, test to see if there is a significant difference in the average sales of the three stores.
(Essay)
4.9/5  (30)
(30)
Exhibit 13-5
Part of an ANOVA table is shown below.  -Refer to Exhibit 13-5. The mean square within treatments (MSE) is
-Refer to Exhibit 13-5. The mean square within treatments (MSE) is
(Multiple Choice)
4.9/5  (43)
(43)
At = 0.05, test to determine if the means of the three populations (from which the following samples are selected) are equal. 
(Essay)
4.9/5  (38)
(38)
The ANOVA procedure is a statistical approach for determining whether or not
(Multiple Choice)
4.8/5  (46)
(46)
Showing 21 - 40 of 125
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)