Exam 13: Experimental Design and Analysis of Variance

Exhibit 13-3 To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. -Refer to Exhibit 13-3. The test statistic to test the null hypothesis equals

Five drivers were selected to test drive 2 makes of automobiles. The following table shows the number of miles per gallon for each driver driving each car. 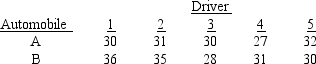Consider the makes of automobiles as treatments and the drivers as blocks, use Excel to test to see if there is any difference in the miles/gallon of the two makes of automobiles. Let $\alpha$ = .05.

Exhibit 13-7 The following is part of an ANOVA table, which was the results of three treatments and a total of 15 observations. -Refer to Exhibit 13-7. The conclusion of the test is that the means

Exhibit 13-7 The following is part of an ANOVA table, which was the results of three treatments and a total of 15 observations. -The critical F value with 8 numerator and 29 denominator degrees of freedom at $\alpha$ = 0.01 is

A research organization wishes to determine whether four brands of batteries for transistor radios perform equally well. Three batteries of each type were randomly selected and installed in the three test radios. The number of hours of use for each battery is given below. a.Use the analysis of variance procedure for completely randomized designs to determine whether there is a significant difference in the mean useful life of the four types of batteries. (Ignore the fact that there are different test radios.) Use the .05 level of significance and be sure to construct the ANOVA table. b. b.Now consider the three different test radios and carry out the analysis of variance procedure for a randomized block design. Include the ANOVA table. c.Compare the results in Parts a and

Exhibit 13-7 The following is part of an ANOVA table, which was the results of three treatments and a total of 15 observations. -Information regarding the ACT scores of samples of students in three different majors are given below. 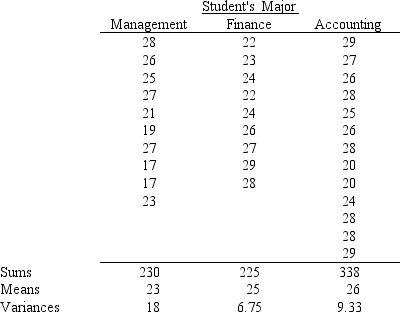a.Set up the ANOVA table for this problem. b.At a 5% level of significance, test to determine whether there is a significant difference in the means of the three populations.

In an analysis of variance where the total sample size for the experiment is n_T and the number of populations is k, the mean square within treatments is

Exhibit 13-7 The following is part of an ANOVA table, which was the results of three treatments and a total of 15 observations. -Three different brands of tires were compared for wear characteristics. For each brand of tire, ten tires were randomly selected and subjected to standard wear testing procedures. The average mileage obtained for each brand of tire and sample standard deviations (both in 1000 miles) are shown below. 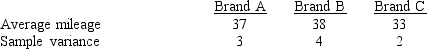Use the above data and test to see if the mean mileage for all three brands of tires is the same. Let Alpha = 0.05.

The number of times each experimental condition is observed in a factorial design is known as

The heating bills for a selected sample of houses using various forms of heating are given below (values are in dollars). 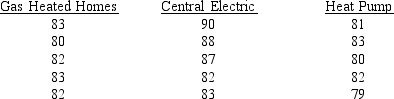At $\mu$ = 0.05, test to see if there is a significant difference among the average bills of the homes.

The variable of interest in an ANOVA procedure is called

Exhibit 13-7 The following is part of an ANOVA table, which was the results of three treatments and a total of 15 observations. -Refer to Exhibit 13-7. The number of degrees of freedom corresponding to between treatments is

Exhibit 13-7 The following is part of an ANOVA table, which was the results of three treatments and a total of 15 observations. -In a completely randomized experimental design, 11 experimental units were used for each of the 3 treatments. Part of the ANOVA table is shown below. 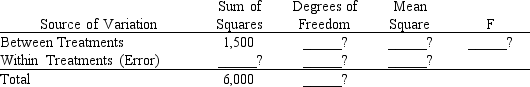a.Fill in the blanks in the above ANOVA table. b.At a 5% level of significance, test to determine whether or not the means of the 3 populations are equal.

In the analysis of variance procedure (ANOVA), factor refers to

Exhibit 13-6 Part of an ANOVA table is shown below. -Refer to Exhibit 13-6. The number of degrees of freedom corresponding to within treatments is

Exhibit 13-6 Part of an ANOVA table is shown below. -Refer to Exhibit 13-6. If at a 5% significance level we want to determine whether or not the means of the populations are equal, the critical value of F is

Exhibit 13-7 The following is part of an ANOVA table, which was the results of three treatments and a total of 15 observations. -MNM, Inc. has three stores located in three different areas. Random samples of the sales of the three stores (in $1,000) are shown below. At a 5% level of significance, test to see if there is a significant difference in the average sales of the three stores. Show your complete work and the ANOVA table. (Please note that the sample sizes are not equal.)

Exhibit 13-3 To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. -Refer to Exhibit 13-3. The mean square between treatments (MSTR) equals

Five drivers were selected to test drive 2 makes of automobiles. The following table shows the number of miles per gallon for each driver driving each car. Consider the makes of automobiles as treatments and the drivers as blocks, test to see if there is any difference in the miles/gallon of the two makes of automobiles. Let $\mu$ = .05.

Exhibit 13-7 The following is part of an ANOVA table, which was the results of three treatments and a total of 15 observations. -In a completely randomized design involving four treatments, the following information is provided. 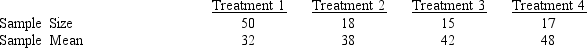The overall mean (the grand mean) for all treatments is