Exam 15: Multiple Regression
Exam 1: Data and Statistics85 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays112 Questions
Exam 3: Descriptive Statistics: Numerical Measures139 Questions
Exam 4: Introduction to Probability129 Questions
Exam 5: Discrete Probability Distributions150 Questions
Exam 6: Continuous Probability Distributions144 Questions
Exam 7: Sampling and Sampling Distributions119 Questions
Exam 8: Interval Estimation118 Questions
Exam 9: Hypothesis Tests118 Questions
Exam 10: Inference About Means and Proportions With Two Populations127 Questions
Exam 11: Inferences About Population Variances113 Questions
Exam 12: Tests of Goodness of Fit, Independence and Multiple Proportions76 Questions
Exam 13: Experimental Design and Analysis of Variance125 Questions
Exam 14: Simple Linear Regression103 Questions
Exam 15: Multiple Regression109 Questions
Exam 16: Regression Analysis: Model Building82 Questions
Exam 17: Time Series Analysis and Forecasting80 Questions
Exam 18: Nonparametric Methods83 Questions
Exam 19: Statistical Methods for Quality Control75 Questions
Exam 20: Decision Analysis71 Questions
Exam 21: Sample Survey68 Questions
Select questions type
Exhibit 15-1
In a regression model involving 44 observations, the following estimated regression equation was obtained. 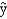 = 29 + 18x1 +43x2 + 87x3
For this model SSR = 600 and SSE = 400.
-Refer to Exhibit 15-1. MSR for this model is
= 29 + 18x1 +43x2 + 87x3
For this model SSR = 600 and SSE = 400.
-Refer to Exhibit 15-1. MSR for this model is
(Multiple Choice)
4.8/5  (36)
(36)
Exhibit 15-8
The following estimated regression model was developed relating yearly income (y in $1,000s) of 30 individuals with their age (x1) and their gender (x2) (0 if male and 1 if female). 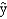 = 30 + 0.7x1 + 3x2
Also provided are SST = 1,200 and SSE = 384.
-Refer to Exhibit 15-8. The model
= 30 + 0.7x1 + 3x2
Also provided are SST = 1,200 and SSE = 384.
-Refer to Exhibit 15-8. The model
(Multiple Choice)
4.7/5  (48)
(48)
Exhibit 15-5
Below you are given a partial Excel output based on a sample of 25 observations.  -Refer to Exhibit 15-5. We want to test whether the parameter 1 is significant. The test statistic equals
-Refer to Exhibit 15-5. We want to test whether the parameter 1 is significant. The test statistic equals
(Multiple Choice)
5.0/5  (30)
(30)
In order to test for the significance of a regression model involving 14 independent variables and 255 observations, the numerator and denominator degrees of freedom (respectively) for the critical value of F are
(Multiple Choice)
4.8/5  (48)
(48)
The Natural Drink Company has developed a regression model relating its sales (y in $10,000s) with four independent variables. The four independent variables are price per unit (PRICE, in dollars), competitor's price (COMPRICE, in dollars), advertising (ADV, in $1,000s) and type of container used (CONTAIN; 1 = Cans and 0 = Bottles). Part of the regression results is shown below. (Assume n = 25) 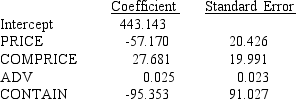 a.If the manufacturer uses can containers, his price is $1.25, advertising $200,000, and his competitor's price is $1.50, what is your estimate of his sales? Give your answer in dollars.
b.Test to see if there is a significant relationship between sales and unit price. Let = 0.05.
c.Test to see if there is a significant relationship between sales and advertising. Let = 0.05.
d.Is the type of container a significant variable? Let = 0.05.
e.Test to see if there is a significant relationship between sales and competitor's price. Let = 0.05.
a.If the manufacturer uses can containers, his price is $1.25, advertising $200,000, and his competitor's price is $1.50, what is your estimate of his sales? Give your answer in dollars.
b.Test to see if there is a significant relationship between sales and unit price. Let = 0.05.
c.Test to see if there is a significant relationship between sales and advertising. Let = 0.05.
d.Is the type of container a significant variable? Let = 0.05.
e.Test to see if there is a significant relationship between sales and competitor's price. Let = 0.05.
(Essay)
4.9/5  (32)
(32)
In a multiple regression analysis SSR = 1,000 and SSE = 200. The F statistic for this model is
(Multiple Choice)
4.7/5  (22)
(22)
A regression model involving 3 independent variables for a sample of 20 periods resulted in the following sum of squares.  a.Compute the coefficient of determination and fully explain its meaning.
b.At = 0.05 level of significance, test to determine whether or not there is a significant relationship between the independent variables and the dependent variable.
a.Compute the coefficient of determination and fully explain its meaning.
b.At = 0.05 level of significance, test to determine whether or not there is a significant relationship between the independent variables and the dependent variable.
(Essay)
4.8/5  (40)
(40)
Exhibit 15-2
A regression model between sales (y in $1,000), unit price (x1 in dollars) and television advertisement (x2 in dollars) resulted in the following function: 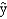 = 7 - 3x1 + 5x2
For this model SSR = 3500, SSE = 1500, and the sample size is 18.
-Refer to Exhibit 15-2. If SSR = 600 and SSE = 300, the test statistic F is
= 7 - 3x1 + 5x2
For this model SSR = 3500, SSE = 1500, and the sample size is 18.
-Refer to Exhibit 15-2. If SSR = 600 and SSE = 300, the test statistic F is
(Multiple Choice)
4.8/5  (43)
(43)
Exhibit 15-1
In a regression model involving 44 observations, the following estimated regression equation was obtained. 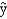 = 29 + 18x1 +43x2 + 87x3
For this model SSR = 600 and SSE = 400.
-Refer to Exhibit 15-1. The coefficient of determination for the above model is
= 29 + 18x1 +43x2 + 87x3
For this model SSR = 600 and SSE = 400.
-Refer to Exhibit 15-1. The coefficient of determination for the above model is
(Multiple Choice)
4.7/5  (40)
(40)
A regression model involving 8 independent variables for a sample of 69 periods resulted in the following sum of squares.SSE = 306
SST = 1800
a.Compute the coefficient of determination.
b.At = 0.05, test to determine whether or not the model is significant.
(Essay)
4.9/5  (36)
(36)
In a multiple regression model, the values of the error term , , are assumed to be
(Multiple Choice)
5.0/5  (33)
(33)
Exhibit 15-3
In a regression model involving 30 observations, the following estimated regression equation was obtained: 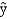 = 17 + 4x1 - 3x2 + 8x3 + 8x4
For this model SSR = 700 and SSE = 100.
-Refer to Exhibit 15-3. The critical F value at 95% confidence is
= 17 + 4x1 - 3x2 + 8x3 + 8x4
For this model SSR = 700 and SSE = 100.
-Refer to Exhibit 15-3. The critical F value at 95% confidence is
(Multiple Choice)
4.9/5  (31)
(31)
Multiple regression analysis was used to study how an individual's income (y in thousands of dollars) is influenced by age (x1 in years), level of education (x2 ranging from 1 to 5), and the person's gender (x3 where 0 =female and 1=male). The following is a partial result of Excel output that was used on a sample of 20 individuals. 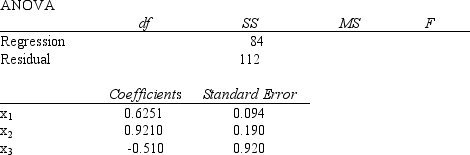 a.Compute the coefficient of determination.
b.Perform a t test and determine whether or not the coefficient of the variable "level of education" (i.e., x2) is significantly different from zero. Let = 0.05.
c.At = 0.05, perform an F test and determine whether or not the regression model is significant.
d.As you note the coefficient of x3 is -0.510. Fully interpret the meaning of this coefficient.
a.Compute the coefficient of determination.
b.Perform a t test and determine whether or not the coefficient of the variable "level of education" (i.e., x2) is significantly different from zero. Let = 0.05.
c.At = 0.05, perform an F test and determine whether or not the regression model is significant.
d.As you note the coefficient of x3 is -0.510. Fully interpret the meaning of this coefficient.
(Essay)
4.8/5  (38)
(38)
Exhibit 15-8
The following estimated regression model was developed relating yearly income (y in $1,000s) of 30 individuals with their age (x1) and their gender (x2) (0 if male and 1 if female). 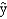 = 30 + 0.7x1 + 3x2
Also provided are SST = 1,200 and SSE = 384.
-In a residual plot that does not suggest we should challenge the assumptions of our regression model, we would expect to see
= 30 + 0.7x1 + 3x2
Also provided are SST = 1,200 and SSE = 384.
-In a residual plot that does not suggest we should challenge the assumptions of our regression model, we would expect to see
(Multiple Choice)
4.8/5  (30)
(30)
The prices of Rawlston, Inc. stock (y) over a period of 12 days, the number of shares (in 100s) of company's stocks sold (x1), and the volume of exchange (in millions) on the New York Stock Exchange (x2) are shown below. 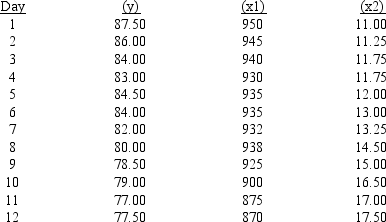 Excel was used to determine the least-squares regression equation. Part of the computer output is shown below.
Excel was used to determine the least-squares regression equation. Part of the computer output is shown below. 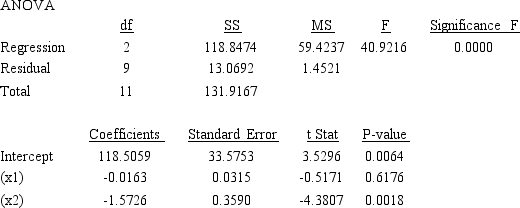 a.Use the output shown above and write an equation that can be used to predict the price of the stock.
b.Interpret the coefficients of the estimated regression equation that you found in Part
c.At 95% confidence, determine which variables are significant and which are not.
d.If in a given day, the number of shares of the company that were sold was 94,500 and the volume of exchange on the New York Stock Exchange was 16 million, what would you expect the price of the stock to be?
a.Use the output shown above and write an equation that can be used to predict the price of the stock.
b.Interpret the coefficients of the estimated regression equation that you found in Part
c.At 95% confidence, determine which variables are significant and which are not.
d.If in a given day, the number of shares of the company that were sold was 94,500 and the volume of exchange on the New York Stock Exchange was 16 million, what would you expect the price of the stock to be?
(Essay)
5.0/5  (27)
(27)
Exhibit 15-8
The following estimated regression model was developed relating yearly income (y in $1,000s) of 30 individuals with their age (x1) and their gender (x2) (0 if male and 1 if female). 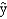 = 30 + 0.7x1 + 3x2
Also provided are SST = 1,200 and SSE = 384.
-The mathematical equation that explains how the dependent variable y is related to several independent variables x1, x2, ..., xp and the error term is
= 30 + 0.7x1 + 3x2
Also provided are SST = 1,200 and SSE = 384.
-The mathematical equation that explains how the dependent variable y is related to several independent variables x1, x2, ..., xp and the error term is
(Multiple Choice)
4.8/5  (29)
(29)
In order to test for the significance of a regression model involving 3 independent variables and 47 observations, the numerator and denominator degrees of freedom (respectively) for the critical value of F are
(Multiple Choice)
4.7/5  (38)
(38)
The correct relationship between SST, SSR, and SSE is given by
(Multiple Choice)
4.8/5  (38)
(38)
In a multiple regression analysis involving 12 independent variables and 166 observations, SSR = 878 and SSE = 122. The coefficient of determination is
(Multiple Choice)
4.8/5  (38)
(38)
Showing 41 - 60 of 109
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)