Exam 8: Techniques of Integration
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
Evaluate the integrals using Integration by Parts, the Substitution Method, or both methods.
A) 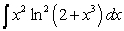 B)
B) 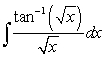
(Essay)
4.9/5  (38)
(38)
Use the substitution 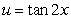 and the trigonometric identity
and the trigonometric identity 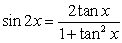 , or reduction formulas as necessary, to calculate the integrals.
A)
, or reduction formulas as necessary, to calculate the integrals.
A) 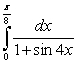 B)
B) 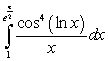
(Essay)
4.8/5  (41)
(41)
The time between customers at a checkout line is a random variable with exponential density. There is a 30% probability of waiting 5 min or more between customers. What is the average time between customers?
(Short Answer)
4.9/5  (30)
(30)
Evaluate the integral using one or two methods, as indicated.
A) 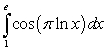 : the Substitution Method followed by Integration by Parts, twice.
B)
: the Substitution Method followed by Integration by Parts, twice.
B) 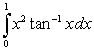 : Integration by Parts followed by the Substitution Method.
: Integration by Parts followed by the Substitution Method.
(Essay)
4.9/5  (37)
(37)
A cereal-packaging company fills boxes on average with 39 oz of cereal. Due to machine error, the actual volume is normally distributed with a standard deviation of
0.2 oz. Let 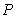 be the probability of a box having less than 38.5 oz. Express
be the probability of a box having less than 38.5 oz. Express 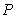 as an integral of an appropriate density function and compute its value numerically.
as an integral of an appropriate density function and compute its value numerically.
(Essay)
4.8/5  (41)
(41)
The height of sixth grade students in a certain class is a random variable  with mean
with mean 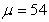 in. Assume the height of the students is normally distributed with standard deviation
in. Assume the height of the students is normally distributed with standard deviation 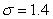 in. Let
in. Let 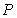 be the probability that a student will be at least
be the probability that a student will be at least 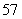 in. tall. Express
in. tall. Express 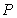 as an integral of an appropriate density function, and compute its value numerically.
as an integral of an appropriate density function, and compute its value numerically.
(Essay)
4.9/5  (38)
(38)
The height of sixth grade students in a class is a random variable 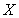 with mean
with mean 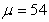 in. Assume the height of the students is normally distributed with standard deviation
in. Assume the height of the students is normally distributed with standard deviation 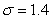 in. Let
in. Let 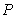 be the probability that a student will be at most
be the probability that a student will be at most 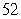 in. tall. Express
in. tall. Express 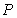 as an integral of an appropriate density function, and compute its value numerically.
as an integral of an appropriate density function, and compute its value numerically.
(Essay)
4.9/5  (38)
(38)
Showing 21 - 40 of 101
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)