Exam 6: Applications of Integration

The base of a certain solid is a plane region R enclosed by the x-axis and the curve $y = 1 - x ^ { 2 }$ . Each cross-section of the solid perpendicular to the y-axis is an isosceles triangle of height 4 with its base lying in R. Find the volume of the solid.

A manufacture has been selling 1000 ceiling fans at $60 each. A market survey indicates that for every $10 that price is reduced, the number of sets sold will increase by 100. Find the demand function and calculate the consumer surplus when the selling price is set at $50.

A supply function is given by $p _ { 3 } ( x ) = 5 + \frac { 1 } { 10 } x$ , where x is the number of units produced. Find the producer surplus when the selling price is $15.

(a) Show that $f ( x ) = \left\{ \begin{array} { l l } 4 x + 12 x ^ { 2 } & \text { if } 0 \leq x \leq \frac { 1 } { 2 } \\0 & \text { otherwise }\end{array} \right.$ is the probability density function of a random variable.(b) What is the mean for this distribution? (c) Calculate the median of $f$

Let $f ( x ) = 6 x ( 1 - x ) , 0 < x < 1$ be the probability density function of a random variable X. Find the mean of the probability density function $f$ .

Find the volume of the solid obtained by rotating the region bounded by xy = 1, y = 1, y = 2 and the y-axis about the x-axis.

Find k so that the function $f ( x ) = \left\{ \begin{array} { l l } k x ( 1 - x ) & \text { if } 0 < x < 1 \\0 & \text { otherwise }\end{array} \right.$ can serve as the probability density function of a random variable X.

Find the x-coordinate x at the centroid of the region bounded by the x-axis and the lines $y = 3 x , \quad x = 2$

Find the volume of the solid obtained when the region bounded by the line $y = 2 x$ , the line $x = 3$ , and the x-axis is rotated about the y-axis.

The volume of the solid obtained by rotating the plane region enclosed by $y = x ^ { 4 } , y = 1 , \text { and } x = 0$ about the y-axis is

Find the y-coordinate of the centroid of the region bounded by the curves $y = x ^ { 2 } , y = 1$

Find the distance traveled by a particle with position $( x , y ) = \left( \cos ^ { 2 } t , \cos t \right)$ as t varies in the time interval $[ 0,4 \pi ]$ . Compare with the length of the curve.

Let $f ( x ) = 6 x ( 1 - x ) , 0 < x < 1$ be the probability density function of a random variable X. Find the median of the probability density function $f$ .

A particle is moving in a straight line and its velocity is given by $v ( t ) = 3 t ^ { 2 } - 12 t + 9,$ where t is measure in seconds and v in meters per second. Find the distance traveled by the particle during the time interval $[ 0,5 ]$ .

The demand function for a certain commodity is $p = 5 - \frac { x } { 10 }$ Find the consumer's surplus when the sales level is 30. Illustrate by drawing the demand curve and identifying the consumer's surplus as an area.

The volume of the solid obtained by rotating the plane region enclosed by $y = \frac { \sin ( 2 x ) } { x } , x = \frac { \pi } { 2 } ,$ the y-axis and the x-axis about the y-axis is

Set up, but do not evaluate, an integral for the length of $y = x ^ { 4 } - x ^ { 2 } , - 1 \leq x \leq 2$

The region R is given by the shaded area in the figure below: 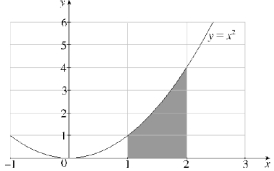(a) Find the area of the shaded region R.(b) Find the volume of the solid obtained by rotating R about (i) the x-axis. (ii) the y-axis. (iii) the line x = 2. (iv) the line y = 4

If $x = \cos 2 t , y = \sin ^ { 2 } t \text { and } ( x , y )$ represents the position of a particle, find the distance the particle travels as t moves from 0 to $\frac { \pi } { 2 } .$

A hemispherical tank with radius 8 feet is filled with water to a depth of 6 feet. Find the work required to empty the tank by pumping the water to the top of the tank.