Exam 6: Applications of Integration
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
The density function for the waiting time at a bank is modeled by and is measured in minutes.(a) Find the median waiting time.(b) Find the mean waiting time.(c) Sketch the graph of the density function showing the median and mean.
(Essay)
4.9/5  (45)
(45)
Find the area of the region bounded by the curve , and the x-axis.
(Multiple Choice)
4.9/5  (43)
(43)
A tank contains water. The end of the tank is vertical and has the shape below. Find the hydrostatic force against the end of the tank. 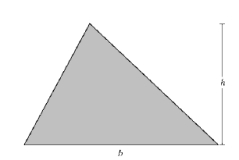
(Essay)
4.8/5  (31)
(31)
Let be the probability density function of a random variable X. Find the median of the probability density function .
(Multiple Choice)
4.8/5  (38)
(38)
Find the volume of the solid obtained when the region bounded by the x-axis, the y-axis, and the line is rotated about the x-axis.
(Multiple Choice)
4.8/5  (35)
(35)
Consider the region R bounded by , and the y-axis.(a) Find the area of R.(b) Find the average height of R.(c) Find the volume, V, of the solid obtained by rotating R about the x-axis.(d) A cross section of the solid generated by part (c) taken perpendicular to the x-axis is a washer. Determine the average area of the cross sections of the solid.
(Essay)
4.9/5  (32)
(32)
If ft-lb of work is needed to stretch a spring a length ft beyond its natural length, find the spring constant.
(Short Answer)
4.8/5  (37)
(37)
Find the x-coordinate of the centroid of the region bounded by the graphs and the x-axis.
(Multiple Choice)
4.8/5  (40)
(40)
Find the volume of the solid obtained when the region bounded by the curves , , and the x-axis is rotated about the line x = - 1.
(Multiple Choice)
4.8/5  (44)
(44)
Let be the probability density function of a random variable T, where t is the time that a customer spends in line at teller's window before being served. What is the probability that a customer will wait more than 10 minutes?
(Essay)
4.8/5  (31)
(31)
Suppose a company has estimated that the marginal cost of manufacturing x pairs of a new line of jeans is (measured in dollars per pair) with a fixed start-up cost of c(0) = 2000. Find the cost of producing the first 1000 pair of jeans.
(Multiple Choice)
4.8/5  (34)
(34)
Consider the region in the xy-plane between and . Find the volume of the solid generated by rotating this region about the x-axis.
(Short Answer)
4.7/5  (38)
(38)
(a) Explain why the function defined by the graph below is a probability density function. 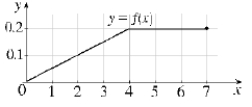 (b) Use the graph to find the following probabilities:
(i) (ii) (c) Calculate the median for this distribution.
(b) Use the graph to find the following probabilities:
(i) (ii) (c) Calculate the median for this distribution.
(Essay)
4.8/5  (35)
(35)
The voltage (in volts) at an electrical outlet is a function of time (in seconds) given by V(t) = V0 cos(120 ) where V0 is a constant representing the maximum voltage.(a) What is the average value of the voltage over one second?
(b) How many times does the voltage reach a maximum in one second?
(c) Define the new function . Compute , the average value of over one cycle.(d) Instead of the average voltage, engineers use the root mean square . Determine Vrms in terms of V0.(e) The standard household voltage in the United Stated is 100 volts. This means that Vrms = 110. What is the value of V0?
(Essay)
4.9/5  (43)
(43)
Express the area of the given region as a definite integral. Do not evaluate. 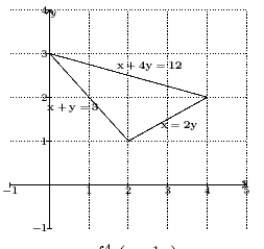
(Essay)
4.8/5  (38)
(38)
Showing 41 - 60 of 189
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)