Exam 9: Assessing Studies Based on Multiple Regression
In the case of errors-in-variables bias,the precise size and direction of the bias depend on
B
You have been hired as a consultant by building contractor,who have been sued by the owners' representatives of a large condominium project for shoddy construction work.In order to assess the damages for the various units,the owners' association sent out a letter to owners and asked if people were willing to make their units available for destructive testing.Destructive testing was conducted in some of these units as a result of the responses.Based on the tests,the owners' association inferred the damage over the entire condo complex.Do you think that the inference is valid in this case? Discuss how proper sampling should proceed in this situation.
This is clearly a case of sample selection bias which leads to bias in the OLS estimator in general.It should be clear that inference cannot be conducted properly,since owners who suspect that their unit is faulty are much more likely to agree to destructive testing of their unit than those who have not experienced any problems.The proportion of units assumed to be faulty in the population is bound to be too large when derived through sampling of this type.
The proper sampling method would be to decide on the units to be tested through random sampling.A random number generator should be used to determine the sampled units.The owners' association must guarantee that the randomly selected units are available for destructive testing.
To analyze the situation of simultaneous causality bias,consider the following system of equations:
Yi = β0 + β1Xi + ui
Xi =  +
+  Yi + vi
Demonstrate the negative correlation between Xi and
Yi + vi
Demonstrate the negative correlation between Xi and  for
for  < 0 ,either through mathematics or by presenting an argument which starts as follows: "Imagine that ui is negative."
< 0 ,either through mathematics or by presenting an argument which starts as follows: "Imagine that ui is negative."
The mathematical derivation of the correlation is given in footnote 3 of Chapter 7 in the textbook.Setting 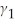 <0 results in a negative correlation between Xi and ui.A negative shock to the first equation yields a lower Y.This in turn increases X in the second equation.Hence there is a negative correlation between Xi and ui.
<0 results in a negative correlation between Xi and ui.A negative shock to the first equation yields a lower Y.This in turn increases X in the second equation.Hence there is a negative correlation between Xi and ui.
Think of three different economic examples where cross-sectional data could be collected.Indicate in each of these cases how you would check if the analysis is externally valid.
In the case of a simple regression,where the independent variable is measured with i.i.d.error,
Macroeconomists who study the determinants of per capita income (the "wealth of nations")have been particularly interested in finding evidence on conditional convergence in the countries of the world.Finding such a result would imply that all countries would end up with the same per capita income once other variables such as saving and population growth rates,education,government policies,etc. ,took on the same value.Unconditional convergence,on the other hand,does not control for these additional variables.
(a)The results of the regression for 104 countries was as follows,  = 0.019 - 0.0006 × RelProd60,R2= 0.00007,SER = 0.016
(0.004)(0.0073),
where g6090 is the average annual growth rate of GDP per worker for the 1960-1990 sample period,and RelProd60 is GDP per worker relative to the United States in 1960.
For the 24 OECD countries in the sample,the output is
= 0.019 - 0.0006 × RelProd60,R2= 0.00007,SER = 0.016
(0.004)(0.0073),
where g6090 is the average annual growth rate of GDP per worker for the 1960-1990 sample period,and RelProd60 is GDP per worker relative to the United States in 1960.
For the 24 OECD countries in the sample,the output is  = 0.048 - 0.0404 RelProd60,R2 = 0.82,SER = 0.0046
(0.004)(0.0063)
Interpret the results and point out the difference with regard to unconditional convergence.
(b)The "beta-convergence" regressions in (a)are of the following type,
= 0.048 - 0.0404 RelProd60,R2 = 0.82,SER = 0.0046
(0.004)(0.0063)
Interpret the results and point out the difference with regard to unconditional convergence.
(b)The "beta-convergence" regressions in (a)are of the following type,  = β0 + β0 ln Yi,0 + ui,t,
where △t ln Yi,t = ln Yi,0 - ln Yi,0,and t and o refer to two time periods,i is the i-th country.
Explain why a significantly negative slope implies convergence (hence the name).
(c)The equation in (b)can be rewritten without any change in information as (ignoring the division by T)
ln Yt = β0 + γ1 ln Y0 + ut
In this form,how would you test for unconditional convergence? What would be the implication for convergence if the slope coefficient were one?
(d)Let's write the equation in (c)as follows:
= β0 + β0 ln Yi,0 + ui,t,
where △t ln Yi,t = ln Yi,0 - ln Yi,0,and t and o refer to two time periods,i is the i-th country.
Explain why a significantly negative slope implies convergence (hence the name).
(c)The equation in (b)can be rewritten without any change in information as (ignoring the division by T)
ln Yt = β0 + γ1 ln Y0 + ut
In this form,how would you test for unconditional convergence? What would be the implication for convergence if the slope coefficient were one?
(d)Let's write the equation in (c)as follows:  and assume that the "~" variables contain measurement errors of the following type,
and assume that the "~" variables contain measurement errors of the following type,  where the "*" variables represent true,or permanent,per capita income components,while v and w are temporary or transitory components.Subtraction of the initial period from the current period then results in
where the "*" variables represent true,or permanent,per capita income components,while v and w are temporary or transitory components.Subtraction of the initial period from the current period then results in  Ignoring,without loss of generality,the constant in the above equation,and making standard assumptions about the error term,one can show that by regressing current per capita income on a constant and the initial period per capita income,the slope behaves as follows:
Ignoring,without loss of generality,the constant in the above equation,and making standard assumptions about the error term,one can show that by regressing current per capita income on a constant and the initial period per capita income,the slope behaves as follows:  Discuss the implications for the convergence results above.
Discuss the implications for the convergence results above.
You have read the analysis in chapter 9 and want to explore the relationship between poverty and test scores.You decide to start your analysis by running a regression of test scores on the percent of students who are eligible to receive a free/reduced price lunch both in California and in Massachusetts.The results are as follows:  CA = 681.44 - 0.610×PctLchCA
(0.99)(0.018)
n = 420,R2 = 0.75,SER = 9.45
CA = 681.44 - 0.610×PctLchCA
(0.99)(0.018)
n = 420,R2 = 0.75,SER = 9.45  MA = 731.89 - 0.788×PctLchMA
(0.95)(0.045)
n = 220,R2 = 0.61,SER = 9.41
Numbers in parenthesis are heteroskedasticity-robust standard errors.
a.Calculate a t-statistic to test whether or not the two slope coefficients are the same.
b.Your textbook compares the slope coefficients for the student-teacher ratio instead of the percent eligible for a free lunch.The authors remark: "Because the two standardized tests are different,the coefficients themselves cannot be compared directly: One point on the Massachusetts test is not the same as one point on the California test." What solution do they suggest?
MA = 731.89 - 0.788×PctLchMA
(0.95)(0.045)
n = 220,R2 = 0.61,SER = 9.41
Numbers in parenthesis are heteroskedasticity-robust standard errors.
a.Calculate a t-statistic to test whether or not the two slope coefficients are the same.
b.Your textbook compares the slope coefficients for the student-teacher ratio instead of the percent eligible for a free lunch.The authors remark: "Because the two standardized tests are different,the coefficients themselves cannot be compared directly: One point on the Massachusetts test is not the same as one point on the California test." What solution do they suggest?
Your textbook uses the following example of simultaneous causality bias of a two equation system:
Yi = β0 + β1Xi + ui
Xi =  +
+  Yi + vi
To be more specific,think of the first equation as a demand equation for a certain good,where Y is the quantity demanded and X is the price.The second equation then represents the supply equation,with a third equation establishing that demand equals supply.Sketch the market outcome over a few periods and explain why it is impossible to identify the demand and supply curves in such a situation.Next assume that an additional variable enters the demand equation: income.In a new graph,draw the initial position of the demand and supply curves and label them D0 and S0.Now allow for income to take on four different values and sketch what happens to the two curves.Is there a pattern that you see which suggests that you might be able to identify one of the two equations with real-life data?
Yi + vi
To be more specific,think of the first equation as a demand equation for a certain good,where Y is the quantity demanded and X is the price.The second equation then represents the supply equation,with a third equation establishing that demand equals supply.Sketch the market outcome over a few periods and explain why it is impossible to identify the demand and supply curves in such a situation.Next assume that an additional variable enters the demand equation: income.In a new graph,draw the initial position of the demand and supply curves and label them D0 and S0.Now allow for income to take on four different values and sketch what happens to the two curves.Is there a pattern that you see which suggests that you might be able to identify one of the two equations with real-life data?
The reliability of a study using multiple regression analysis depends on all of the following with the exception of
Your textbook states that correlation of the error term across observations "will not happen if the data are obtained by sampling at random from the population." However,in one famous study of the electric utility industry,the observations were listed by the size of the output level,from smallest to largest.The pattern of the residuals was as shown in the figure.  What does this pattern suggest to you?
What does this pattern suggest to you?
A professor in your microeconomics lectures derived a labor demand curve in the lecture.Given some reasonable assumptions,she showed that the demand for labor depends negatively on the real wage.You want to put this hypothesis to the test ("show me")and collect data on employment and real wages for a certain industry.You try to estimate the labor demand curve but find no relationship between the two variables.Is economic theory wrong? Explain.
A survey of earnings contains an unusually high fraction of individuals who state their weekly earnings in 100s,such as 300,400,500,etc.This is an example of
You have decided to analyze the year-to-year variation in temperature data.Specifically you want to use this year's temperature to predict next year's temperature for certain cities.As a result,you collect the daily high temperature (Temp)for 100 randomly selected days in a given year for three United States cities: Boston,Chicago,and Los Angeles.You then repeat the exercise for the following year.The regression results are as follows (heteroskedasticity-robust standard errors in parentheses):  = 18.19 + 0.75 ×
= 18.19 + 0.75 ×  ;R2 = 0.62,SER = 12.33
(6.46)(0.10)
;R2 = 0.62,SER = 12.33
(6.46)(0.10)  = 2.47 + 0.95 ×
= 2.47 + 0.95 ×  ;R2 = 0.93,SER = 5.85
(3.98)(0.05)
;R2 = 0.93,SER = 5.85
(3.98)(0.05)  = 37.54 + 0.44 ×
= 37.54 + 0.44 ×  ;R2 = 0.18,SER = 7.17
(15.33)(0.22)
(a)What is the prediction of the above regression for Los Angeles if the temperature in the previous year was 75 degrees? What would be the prediction for Boston?
(b)Assume that the previous year's temperature gives accurate predictions,on average,for this year's temperature.What values would you expect in this case for the intercept and slope? Sketch how each of the above regressions behaves compared to this line.
(c)After reflecting on the results a bit,you consider the following explanation for the above results.Daily high temperatures on any given date are measured with error in the following sense: for any given day in any of the three cities,say January 28,there is a true underlying seasonal temperature (X),but each year there are different temporary weather patterns (v,w)which result in a temperature
;R2 = 0.18,SER = 7.17
(15.33)(0.22)
(a)What is the prediction of the above regression for Los Angeles if the temperature in the previous year was 75 degrees? What would be the prediction for Boston?
(b)Assume that the previous year's temperature gives accurate predictions,on average,for this year's temperature.What values would you expect in this case for the intercept and slope? Sketch how each of the above regressions behaves compared to this line.
(c)After reflecting on the results a bit,you consider the following explanation for the above results.Daily high temperatures on any given date are measured with error in the following sense: for any given day in any of the three cities,say January 28,there is a true underlying seasonal temperature (X),but each year there are different temporary weather patterns (v,w)which result in a temperature  different from X.For the two years in your data set,the situation can be described as follows:
different from X.For the two years in your data set,the situation can be described as follows:  = X + vt and
= X + vt and  = X + wt
Subtracting
= X + wt
Subtracting  from
from  ,you get
,you get  =
=  + wt - vt.Hence the population parameter for the intercept and slope are zero and one,as expected.Show that the OLS estimator for the slope is inconsistent,where
+ wt - vt.Hence the population parameter for the intercept and slope are zero and one,as expected.Show that the OLS estimator for the slope is inconsistent,where  (d)Use the formula above to explain the differences in the results for the three cities.Is your mathematical explanation intuitively plausible?
(d)Use the formula above to explain the differences in the results for the three cities.Is your mathematical explanation intuitively plausible?
In the simple,one-explanatory variable,errors-in-variables model,the OLS estimator for the slope is inconsistent.The textbook derived the following result  .
Show that the OLS estimator for the intercept behaves as follows in large samples:
.
Show that the OLS estimator for the intercept behaves as follows in large samples:  where
where 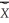

 .
.
Assume the following model of the labor market:
Nd = β0 + β1  + u
Ns = γ0 + γ1
+ u
Ns = γ0 + γ1  + v
Nd = Ns = N
where N is employment, (W/P)is the real wage in the labor market,and u and v are determinants other than the real wage which affect labor demand and labor supply (respectively).Let
E(u)= E(v)= 0;var(u)=
+ v
Nd = Ns = N
where N is employment, (W/P)is the real wage in the labor market,and u and v are determinants other than the real wage which affect labor demand and labor supply (respectively).Let
E(u)= E(v)= 0;var(u)=  ;var(v)=
;var(v)= 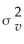 ;cov(u,v)= 0
Assume that you had collected data on employment and the real wage from a random sample of observations and estimated a regression of employment on the real wage (employment being the regressand and the real wage being the regressor).It is easy but tedious to show that
;cov(u,v)= 0
Assume that you had collected data on employment and the real wage from a random sample of observations and estimated a regression of employment on the real wage (employment being the regressand and the real wage being the regressor).It is easy but tedious to show that  > 0
since the slope of the labor supply function is positive and the slope of the labor demand function is negative.Hence,in general,you will not find the correct answer even in large samples.
a.What is this bias referred to?
b.What would the relationship between the variance of the labor supply/demand shift variable have to be for the bias to disappear?
c.Give an intuitive answer why the bias would disappear in that situation.Draw a graph to illustrate your argument.
> 0
since the slope of the labor supply function is positive and the slope of the labor demand function is negative.Hence,in general,you will not find the correct answer even in large samples.
a.What is this bias referred to?
b.What would the relationship between the variance of the labor supply/demand shift variable have to be for the bias to disappear?
c.Give an intuitive answer why the bias would disappear in that situation.Draw a graph to illustrate your argument.
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)