Exam 6: Linear Regression With Multiple Regressors
Assume that you have collected cross-sectional data for average hourly earnings (ahe),the number of years of education (educ)and gender of the individuals (you have coded individuals as "1" if they are female and "0" if they are male;the name of the resulting variable is DFemme).
Having faced recent tuition hikes at your university,you are interested in the return to education,that is,how much more will you earn extra for an additional year of being at your institution.To investigate this question,you run the following regression:  = -4.58 + 1.71×educ
N = 14,925,R2 = 0.18,SER = 9.30
a.Interpret the regression output.
b.Being a female,you wonder how these results are affected if you entered a binary variable (DFemme),which takes on the value of "1" if the individual is a female,and is "0" for males.The result is as follows:
= -4.58 + 1.71×educ
N = 14,925,R2 = 0.18,SER = 9.30
a.Interpret the regression output.
b.Being a female,you wonder how these results are affected if you entered a binary variable (DFemme),which takes on the value of "1" if the individual is a female,and is "0" for males.The result is as follows:  = -3.44 - 4.09×DFemme + 1.76×educ
N = 14,925,R2 = 0.22,SER = 9.08
Does it make sense that the standard error of the regression decreased while the regression R2 increased?
c.Do you think that the regression you estimated first suffered from omitted variable bias?
= -3.44 - 4.09×DFemme + 1.76×educ
N = 14,925,R2 = 0.22,SER = 9.08
Does it make sense that the standard error of the regression decreased while the regression R2 increased?
c.Do you think that the regression you estimated first suffered from omitted variable bias?
a.For every additional year of education,you receive $1.71 additional earnings.It is best not to interpret the intercept,since there are no (or extremely few)observations at the origin.
b.The regression R2 cannot decrease if you add an explanatory variable.If the additional variable does not contribute anything to the fit,then this measure will remain the same.However,in practice,this does not happen.The standard error is a measure of the SSR,and these will almost always decrease with the addition of an explanatory variable.As a result,the observed pattern in the two statistics is to be expected.
c.There are two conditions for omitted variable bias to be present.First,DFemme must be a determinant of ahe;and second,it must be correlated with educ.Given that you have not learned how to test for statistical significance in the multiple regression model,the first question is hard to determine at this point.However,you might argue that the coefficient seems large and that you have read elsewhere that there is evidence of females earning less using this type of equation.With regard to the second question,you could argue that the coefficient on educ has changed somewhat,although the increase does not seem to be large ($0.05).For there to be a correlation between education and the binary female variable,you would have to argue that males and females receive years of education.Either way,the omitted variable bias in the first equation does not appear to be large.
You have obtained data on test scores and student-teacher ratios in region A and region B of your state.Region B,on average,has lower student-teacher ratios than region A.You decide to run the following regression  where
where  is the class size in region A,
is the class size in region A,  is the difference in class size between region A and B,and
is the difference in class size between region A and B,and  is the class size in region B.Your regression package shows a message indicating that it cannot estimate the above equation.What is the problem here and how can it be fixed?
is the class size in region B.Your regression package shows a message indicating that it cannot estimate the above equation.What is the problem here and how can it be fixed?
There is perfect multicollinearity present since one of the three explanatory variables can always be expressed linearly in terms of the other two.Hence there are not really three pieces of independent information contained in the three explanatory variables.Dropping one of the three will solve the problem.
In the multiple regression model Yi = β0 + β1X1i+ β2 X2i + ...+ βkXki + ui,i = 1,... ,n,the OLS estimators are obtained by minimizing the sum of
A
In the multiple regression with two explanatory variables,show that the TSS can still be decomposed into the ESS and the RSS.
You try to establish that there is a positive relationship between the use of a fertilizer and the growth of a certain plant.Set up the design of an experiment to establish the relationship,paying particular attention to relevant control variables.Discuss in this context the effect of omitted variable bias.
You have collected data on individuals and their attributes.Consequently you have generated several binary variables,which take on a value of "1" if the individual has that characteristic and are "0" otherwise.One example is the binary variable DMarr which is "1" for married individuals and "0" for non-married variables.If you run the following regression:
ahei= β0 + β1×educi + β2×DMarri + ui
a.What is the interpretation for β2?
b.You are interested in directly observing the effect that being non-married ("single")has on earnings,controlling for years of education.Instead of recording all observations such that they are "1" for a not married individual and "0" for a married person,how can you generate such a variable (DSingle)through a simple command in your regression program?
Your econometrics textbook stated that there will be omitted variable bias in the OLS estimator unless the included regressor,X,is uncorrelated with the omitted variable or the omitted variable is not a determinant of the dependent variable,Y.Give an intuitive explanation for these two conditions.
You would like to find the effect of gender and marital status on earnings.As a result,you consider running the following regression:
ahei= β0 + β1×DFemmei + β2×DMarri + β3×DSinglei + β4×educi+...+ ui
Where ahe is average hourly earnings,DFemme is a binary variable which takes on the value of "1" if the individual is a female and is "0" otherwise,DMarr is a binary variable which takes on the value of "1" if the individual is married and is "0" otherwise,DSingle takes on the value of "1" if the individual is not married and is "0" otherwise.The regression program which you are using either returns a message that the equation cannot be estimated or drops one of the coefficients.Why do you think that is?
(Requires Calculus)For the simple linear regression model of Chapter 4,  ,the OLS estimator for the intercept was
,the OLS estimator for the intercept was  ,and
,and  .Intuitively,the OLS estimators for the regression model
.Intuitively,the OLS estimators for the regression model 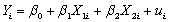 might be
might be  and
and  .By minimizing the prediction mistakes of the regression model with two explanatory variables,show that this cannot be the case.
.By minimizing the prediction mistakes of the regression model with two explanatory variables,show that this cannot be the case.
One of your peers wants to analyze whether or not participating in varsity sports lowers or increases the GPA of students.She decides to collect data from 110 male and female students on their GPA and the number of hours they spend participating in varsity sports.The coefficient in the simple regression function turns out to be significantly negative,using the t-statistic and carrying out the appropriate hypothesis test.Upon reflection,she is concerned that she did not ask the students in her sample whether or not they were female or male.You point out to her that you are more concerned about the effect of omitted variables in her regression,such as the incoming SAT score of the students,and whether or not they are in a major from a high/low grading department.Elaborate on your argument.
You have collected data for 104 countries to address the difficult questions of the determinants for differences in the standard of living among the countries of the world.You recall from your macroeconomics lectures that the neoclassical growth model suggests that output per worker (per capita income)levels are determined by,among others,the saving rate and population growth rate.To test the predictions of this growth model,you run the following regression:  = 0.339 - 12.894 × n + 1.397 × SK,
= 0.339 - 12.894 × n + 1.397 × SK,  =0.621,SER = 0.177
where RelPersInc is GDP per worker relative to the United States,n is the average population growth rate,1980-1990,and SK is the average investment share of GDP from 1960 to 1990 (remember investment equals saving).
(a)Interpret the results.Do the signs correspond to what you expected them to be? Explain.
(b)You remember that human capital in addition to physical capital also plays a role in determining the standard of living of a country.You therefore collect additional data on the average educational attainment in years for 1985,and add this variable (Educ)to the above regression.This results in the modified regression output:
=0.621,SER = 0.177
where RelPersInc is GDP per worker relative to the United States,n is the average population growth rate,1980-1990,and SK is the average investment share of GDP from 1960 to 1990 (remember investment equals saving).
(a)Interpret the results.Do the signs correspond to what you expected them to be? Explain.
(b)You remember that human capital in addition to physical capital also plays a role in determining the standard of living of a country.You therefore collect additional data on the average educational attainment in years for 1985,and add this variable (Educ)to the above regression.This results in the modified regression output:  = 0.046 - 5.869 × n + 0.738 × SK + 0.055 × Educ,
= 0.046 - 5.869 × n + 0.738 × SK + 0.055 × Educ,  =0.775,SER = 0.1377
How has the inclusion of Educ affected your previous results?
(c)Upon checking the regression output,you realize that there are only 86 observations,since data for Educ is not available for all 104 countries in your sample.Do you have to modify some of your statements in (d)?
(d)Brazil has the following values in your sample: RelPersInc = 0.30,n = 0.021,SK = 0.169,Educ = 3.5.Does your equation overpredict or underpredict the relative GDP per worker? What would happen to this result if Brazil managed to double the average educational attainment?
=0.775,SER = 0.1377
How has the inclusion of Educ affected your previous results?
(c)Upon checking the regression output,you realize that there are only 86 observations,since data for Educ is not available for all 104 countries in your sample.Do you have to modify some of your statements in (d)?
(d)Brazil has the following values in your sample: RelPersInc = 0.30,n = 0.021,SK = 0.169,Educ = 3.5.Does your equation overpredict or underpredict the relative GDP per worker? What would happen to this result if Brazil managed to double the average educational attainment?
Females,on average,are shorter and weigh less than males.One of your friends,who is a pre-med student,tells you that in addition,females will weigh less for a given height.To test this hypothesis,you collect height and weight of 29 female and 81 male students at your university.A regression of the weight on a constant,height,and a binary variable,which takes a value of one for females and is zero otherwise,yields the following result: 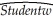 = -229.21 - 6.36 × Female + 5.58 × Height,
= -229.21 - 6.36 × Female + 5.58 × Height,  =0.50,SER = 20.99
where Studentw is weight measured in pounds and Height is measured in inches.
(a)Interpret the results.Does it make sense to have a negative intercept?
(b)You decide that in order to give an interpretation to the intercept you should rescale the height variable.One possibility is to subtract 5 ft.or 60 inches from your Height,because the minimum height in your data set is 62 inches.The resulting new intercept is now 105.58.Can you interpret this number now? Do you thing that the regression
=0.50,SER = 20.99
where Studentw is weight measured in pounds and Height is measured in inches.
(a)Interpret the results.Does it make sense to have a negative intercept?
(b)You decide that in order to give an interpretation to the intercept you should rescale the height variable.One possibility is to subtract 5 ft.or 60 inches from your Height,because the minimum height in your data set is 62 inches.The resulting new intercept is now 105.58.Can you interpret this number now? Do you thing that the regression  has changed? What about the standard error of the regression?
(c)You have learned that correlation does not imply causation.Although this is true mathematically,does this always apply?
has changed? What about the standard error of the regression?
(c)You have learned that correlation does not imply causation.Although this is true mathematically,does this always apply?
In the process of collecting weight and height data from 29 female and 81 male students at your university,you also asked the students for the number of siblings they have.Although it was not quite clear to you initially what you would use that variable for,you construct a new theory that suggests that children who have more siblings come from poorer families and will have to share the food on the table.Although a friend tells you that this theory does not pass the "straight-face" test,you decide to hypothesize that peers with many siblings will weigh less,on average,for a given height.In addition,you believe that the muscle/fat tissue composition of male bodies suggests that females will weigh less,on average,for a given height.To test these theories,you perform the following regression: 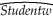 = -229.92 - 6.52 × Female + 0.51 × Sibs+ 5.58 × Height,
= -229.92 - 6.52 × Female + 0.51 × Sibs+ 5.58 × Height,  =0.50,SER = 21.08
where Studentw is in pounds,Height is in inches,Female takes a value of 1 for females and is 0 otherwise,Sibs is the number of siblings.
Interpret the regression results.
=0.50,SER = 21.08
where Studentw is in pounds,Height is in inches,Female takes a value of 1 for females and is 0 otherwise,Sibs is the number of siblings.
Interpret the regression results.
You have collected a sub-sample from the Current Population Survey for the western region of the United States.Running a regression of average hourly earnings (ahe)on an intercept only,you get the following result:  =
=  0 = 18.58
a.Interpret the result.
b.You decide to include a single explanatory variable without an intercept.The binary variable DFemme takes on a value of "1" for females but is "0" otherwise.The regression result changes as follows:
0 = 18.58
a.Interpret the result.
b.You decide to include a single explanatory variable without an intercept.The binary variable DFemme takes on a value of "1" for females but is "0" otherwise.The regression result changes as follows:  =
=  1×DFemme = 16.50×DFemme
What is the interpretation now?
c.You generate a new binary variable DMale by subtracting DFemme from 1,and run the new regression:
1×DFemme = 16.50×DFemme
What is the interpretation now?
c.You generate a new binary variable DMale by subtracting DFemme from 1,and run the new regression:  =
=  2×DMale = 20.09×DMale
What is the interpretation of the coefficient now?
d.After thinking about the above results,you recognize that you could have generated the last two results either by running a regression on both binary variables,or on an intercept and one of the binary variables.What would the results have been?
2×DMale = 20.09×DMale
What is the interpretation of the coefficient now?
d.After thinking about the above results,you recognize that you could have generated the last two results either by running a regression on both binary variables,or on an intercept and one of the binary variables.What would the results have been?
When there are omitted variables in the regression,which are determinants of the dependent variable,then
Consider the following earnings function:
ahei= β0 + β1×DFemmei + β2×educi+...+ ui
versus the alternative specification
ahei= γ0 × DMale + γ1×DFemmei + γ2×educi+...+ ui
where ahe is average hourly earnings,DFemme is a binary variable which takes on the value of "1" if the individual is a female and is "0" otherwise,educ measures the years of education,and DMale is a binary variable which takes on the value of "1" if the individual is a male and is "0" otherwise.There may be additional explanatory variables in the equation.
a.How do the βs and γs compare? Putting it differently,having estimated the coefficients in the first equation,can you derive the coefficients in the second equation without re-estimating the regression?
b.Will the goodness of fit measures,such as the regression R2,differ between the two equations?
c.What is the reason why economists typically prefer the second specification over the first?
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)