Exam 11: Regression With a Binary Dependent Variable

(Requires material from Section 11.3 - possibly skipped)For the measure of fit in your regression model with a binary dependent variable,you can meaningfully use the

A study investigated the impact of house price appreciation on household mobility.The underlying idea was that if a house were viewed as one part of the household's portfolio,then changes in the value of the house,relative to other portfolio items,should result in investment decisions altering the current portfolio.Using 5,162 observations,the logit equation was estimated as shown in the table,where the limited dependent variable is one if the household moved in 1978 and is zero if the household did not move: where male,black,married78,and marriage change are binary variables.They indicate,respectively,if the entity was a male-headed household,a black household,was married,and whether a change in marital status occurred between 1977 and 1978.A7983 is the appreciation rate for each house from 1979 to 1983 minus the SMSA-wide rate of appreciation for the same time period,and PNRN is a predicted appreciation rate for the unit minus the national average rate. (a)Interpret the results.Comment on the statistical significance of the coefficients.Do the slope coefficients lend themselves to easy interpretation? (b)The mean values for the regressors are as shown in the accompanying table. Taking the coefficients at face value and using the sample means,calculate the probability of a household moving. (c)Given this probability,what would be the effect of a decrease in the predicted appreciation rate of 20 percent,that is A7983 = -0.20?

(Requires Appendix material)The following are examples of limited dependent variables,with the exception of

The logit model can be estimated and yields consistent estimates if you are using

In the binary dependent variable model,a predicted value of 0.6 means that

The following problems could be analyzed using probit and logit estimation with the exception of whether or not

The estimated logit regression in your textbook is = F(-4.13 + 5.37 P/Iratio + 1.27 black) Is there a meaningful interpretation to the slope for the P/I Ratio? Calculate the increase of a rejection probability for both blacks and whites as the P/I Ratio increases from 0.1 to 0.2.Repeat the exercise for an increase from 0.65 to 0.75.Why is the increase in the probability higher for blacks at the smaller value of the P/I Ratio but higher for whites at the larger P/I Ratio?

To measure the fit of the probit model,you should:

E(Y X1,... ,Xk)= Pr(Y = 1 X1,... ,Xk)means that

Sketch the regression line for the linear probability model with a single regressor.Indicate for which values of the slope and intercept the predictions will be above one and below zero.Can you rule out homoskedasticity in the error terms with certainty here?

A study tried to find the determinants of the increase in the number of households headed by a female.Using 1940 and 1960 historical census data,a logit model was estimated to predict whether a woman is the head of a household (living on her own)or whether she is living within another's household.The limited dependent variable takes on a value of one if the female lives on her own and is zero if she shares housing.The results for 1960 using 6,051 observations on prime-age whites and 1,294 on nonwhites were as shown in the table: where age is measured in years,education is years of schooling of the family head,farm status is a binary variable taking the value of one if the family head lived on a farm,south is a binary variable for living in a certain region of the country,expected family earnings was generated from a separate OLS regression to predict earnings from a set of regressors,and family composition refers to the number of family members under the age of 18 divided by the total number in the family. The mean values for the variables were as shown in the table. (a)Interpret the results.Do the coefficients have the expected signs? Why do you think age was entered both in levels and in squares? (b)Calculate the difference in the predicted probability between whites and nonwhites at the sample mean values of the explanatory variables.Why do you think the study did not combine the observations and allowed for a nonwhite binary variable to enter? (c)What would be the effect on the probability of a nonwhite woman living on her own,if education and family composition were changed from their current mean to the mean of whites,while all other variables were left unchanged at the nonwhite mean values?

In the probit model Pr(Y = 1 X1,X2,... ,Xk)= Φ(β0 + β1X1 + βxX2 + ...+ βkXk),

The population logit model of the binary dependent variable Y with a single regressor is Pr(Y=1 X1)= . Logistic functions also play a role in econometrics when the dependent variable is not a binary variable.For example,the demand for televisions sets per household may be a function of income,but there is a saturation or satiation level per household,so that a linear specification may not be appropriate.Given the regression model Yi = + ui, sketch the regression line.How would you go about estimating the coefficients?

(Requires Advanced material)Only one of the following models can be estimated by OLS:

Besides maximum likelihood estimation of the logit and probit model,your textbook mentions that the model can also be estimated by nonlinear least squares.Construct the sum of squared prediction mistakes and suggest how computer algorithms go about finding the coefficient values that minimize the function.You may want to use an analogy where you place yourself into a mountain range at night with a flashlight shining at your feet.Your task is to find the lowest point in the valley.You have two choices to make: the direction you are walking in and the step length.Describe how you will proceed to find the bottom of the valley.Once you find the lowest point,is there any guarantee that this is the lowest point of all valleys? What should you do to assure this?

The estimated logit regression in your textbook is = F(-4.13 + 5.37 P/Iratio + 1.27 black) Using a spreadsheet program,such as Excel,generate a table with predicted probabilities for both whites and blacks using P/I Ratio values between 0 and 1 and increments of 0.05.

When estimating probit and logit models,

The logit regression (11.10)on page 393 of your textbook reads: = F(-4.13 + 5.37 P/Iratio + 1.27 black) (a)Using a spreadsheet program such as Excel,plot the following logistic regression function with a single X, 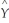i = where 0 = -4.13, 1 = 5.37, 2 = 1.27.Enter values for X1 in the first column starting from 0 and then increment these by 0.1 until you reach 2.0.Let X2 be 0 at first.Then enter the logistic function formula in the next column.Next allow X2 to be 1 and calculate the new values for the logistic function in the third column.Finally produce the predicted probabilities for both blacks and whites,connecting the predicted values with a line. (b)Using the same spreadsheet calculations,list how the probability increases for blacks and for whites as the P/I ratio increases from 0.5 to 0.6. (c)What is the difference in the rejection probability between blacks and whites for a P/I ratio of 0.5 and for 0.9? Why is the difference smaller for the higher value here? (d)Table 11.2 on page 401 of your textbook lists logit regressions (column 2)with further explanatory variables.Given that you can only produce simple plots in two dimensions,how would you proceed in (a)above if there were more than a single explanatory variable?

Your textbook plots the estimated regression function produced by the probit regression of deny on P/I ratio.The estimated probit regression function has a stretched "S" shape given that the coefficient on the P/I ratio is positive.Consider a probit regression function with a negative coefficient.The shape would

(Requires Appendix material and Calculus)The logarithm of the likelihood function (L)for estimating the population mean and variance for an i.i.d.normal sample is as follows (note that taking the logarithm of the likelihood function simplifies maximization.It is a monotonic transformation of the likelihood function,meaning that this transformation does not affect the choice of maximum): L = - log(2πσ2)- Derive the maximum likelihood estimator for the mean and the variance.How do they differ,if at all,from the OLS estimator? Given that the OLS estimators are unbiased,what can you say about the maximum likelihood estimators here? Is the estimator for the variance consistent?