Exam 18: The Theory of Multiple Regression
Exam 1: Economic Questions and Data17 Questions
Exam 2: Review of Probability71 Questions
Exam 3: Review of Statistics63 Questions
Exam 4: Linear Regression With One Regressor65 Questions
Exam 5: Regression With a Single Regressor: Hypothesis Tests and Confidence Intervals59 Questions
Exam 6: Linear Regression With Multiple Regressors65 Questions
Exam 7: Hypothesis Tests and Confidence Intervals in Multiple Regression65 Questions
Exam 8: Nonlinear Regression Functions62 Questions
Exam 9: Assessing Studies Based on Multiple Regression65 Questions
Exam 10: Regression With Panel Data50 Questions
Exam 11: Regression With a Binary Dependent Variable50 Questions
Exam 12: Instrumental Variables Regression50 Questions
Exam 13: Experiments and Quasi-Experiments50 Questions
Exam 14: Introduction to Time Series Regression and Forecasting50 Questions
Exam 15: Estimation of Dynamic Causal Effects50 Questions
Exam 16: Additional Topics in Time Series Regression50 Questions
Exam 17: The Theory of Linear Regression With One Regressor49 Questions
Exam 18: The Theory of Multiple Regression50 Questions
Select questions type
The Gauss-Markov theorem for multiple regression proves that
Free
(Multiple Choice)
4.7/5  (38)
(38)
Correct Answer:
B
Your textbook shows that the following matrix (Mx = In - Px)is a symmetric idempotent matrix.Consider a different Matrix A,which is defined as follows: A = I -  ιι' and ι =
ιι' and ι =  a.Show what the elements of A look like.
b.Show that A is a symmetric idempotent matrix
c.Show that Aι = 0.
d.Show that A
a.Show what the elements of A look like.
b.Show that A is a symmetric idempotent matrix
c.Show that Aι = 0.
d.Show that A  =
=  ,where
,where  is the vector of OLS residuals from a multiple regression.
is the vector of OLS residuals from a multiple regression.
Free
(Essay)
4.8/5  (44)
(44)
Correct Answer:
a.A = 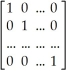 -
- 
 =
= 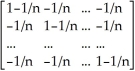 b.A' =
b.A' = 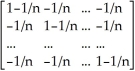 ' =
' = 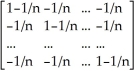 = A
= A
A×A =(I -  ιι')×(I -
ιι')×(I -  ιι')= (I -
ιι')= (I -  ιι' -
ιι' -  ιι' +
ιι' + 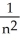 ιι' ιι')
ιι' ιι')
But ιι' ιι' =  ×
×  =
=  ,and
,and 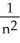
 =
= 
 =
=  ιι'
ιι'
This means that the last two terms in the above equation cancel each other,and therefore A×A = A,that is,A is idempotent.
c.Aι = (I -  ιι')ι = ι -
ιι')ι = ι -  ιι' ι = 0 since ιι' = n
ιι' ι = 0 since ιι' = n
d.A  = (I -
= (I -  ιι')
ιι')  =
=  -
-  ιι'
ιι'  =
=  since ι'
since ι'  = 0
= 0
The multiple regression model in matrix form Y = Xβ + U can also be written as
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
D
In Chapter 10 of your textbook,panel data estimation was introduced.Panel data consist of observations on the same n entities at two or more time periods T.For two variables,you have
(Xit,Yit),i = 1,... ,n and t = 1,... ,T
where n could be the U.S.states.The example in Chapter 10 used annual data from 1982 to 1988 for the fatality rate and beer taxes.Estimation by OLS,in essence,involved "stacking" the data.
(a)What would the variance-covariance matrix of the errors look like in this case if you allowed for homoskedasticity-only standard errors? What is its order? Use an example of a linear regression with one regressor of 4 U.S.states and 3 time periods.
(b)Does it make sense that errors in New Hampshire,say,are uncorrelated with errors in Massachusetts during the same time period ("contemporaneously")? Give examples why this correlation might not be zero.
(c)If this correlation was known,could you find an estimator which was more efficient than OLS?
(Essay)
4.8/5  (31)
(31)
Write the following four restrictions in the form Rβ = r,where the hypotheses are to be tested simultaneously.
β3 = 2β5,
β1 + β2 = 1,
β4 = 0,
β2 = -β6.
Can you write the following restriction β2 = -  in the same format? Why not?
in the same format? Why not?
(Essay)
4.8/5  (41)
(41)
The GLS assumptions include all of the following,with the exception of
(Multiple Choice)
4.8/5  (30)
(30)
Prove that under the extended least squares assumptions the OLS estimator  is unbiased and that its variance-covariance matrix is
is unbiased and that its variance-covariance matrix is  (X'X)-1.
(X'X)-1.
(Essay)
4.9/5  (36)
(36)
Consider the multiple regression model from Chapter 5,where k = 2 and the assumptions of the multiple regression model hold.
(a)Show what the X matrix and the β vector would look like in this case.
(b)Having collected data for 104 countries of the world from the Penn World Tables,you want to estimate the effect of the population growth rate (X1i)and the saving rate (X2i)(average investment share of GDP from 1980 to 1990)on GDP per worker (relative to the U.S. )in 1990.What are your expected signs for the regression coefficient? What is the order of the (X'X)here?
(c)You are asked to find the OLS estimator for the intercept and slope in this model using the
formula  = (X'X)-1 X'Y.Since you are more comfortable in inverting a 2×2 matrix (the inverse of a 2×2 matrix is,
= (X'X)-1 X'Y.Since you are more comfortable in inverting a 2×2 matrix (the inverse of a 2×2 matrix is,  =
= 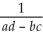
 )
you decide to write the multiple regression model in deviations from mean form.Show what the X matrix,the (X'X)matrix,and the X'Y matrix would look like now.
(Hint: use small letters to indicate deviations from mean,i.e. ,zi = Zi -
)
you decide to write the multiple regression model in deviations from mean form.Show what the X matrix,the (X'X)matrix,and the X'Y matrix would look like now.
(Hint: use small letters to indicate deviations from mean,i.e. ,zi = Zi -  and note that
Yi =
and note that
Yi =  0 +
0 +  1X1i +
1X1i +  2X2i +
2X2i +  i
i  =
= 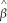 0 +
0 +  1
1  1 +
1 + 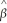 2
2  2.
Subtracting the second equation from the first,you get
yi =
2.
Subtracting the second equation from the first,you get
yi =  1x1i +
1x1i +  2x2i +
2x2i +  i)
(d)Show that the slope for the population growth rate is given by
i)
(d)Show that the slope for the population growth rate is given by 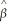 1 =
1 =  (e)The various sums needed to calculate the OLS estimates are given below:
(e)The various sums needed to calculate the OLS estimates are given below: 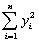 = 8.3103;
= 8.3103;  = .0122;
= .0122; 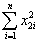 = 0.6422
= 0.6422  = -0.2304;
= -0.2304; 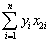 = 1.5676;
= 1.5676;  = -0.0520
Find the numerical values for the effect of population growth and the saving rate on per capita income and interpret these.
(f)Indicate how you would find the intercept in the above case.Is this coefficient of interest in the interpretation of the determinants of per capita income? If not,then why estimate it?
= -0.0520
Find the numerical values for the effect of population growth and the saving rate on per capita income and interpret these.
(f)Indicate how you would find the intercept in the above case.Is this coefficient of interest in the interpretation of the determinants of per capita income? If not,then why estimate it?
(Essay)
5.0/5  (40)
(40)
The extended least squares assumptions in the multiple regression model include four assumptions from Chapter 6 (ui has conditional mean zero; (Xi,Yi),i = 1,…,n are i.i.d.draws from their joint distribution;Xi and ui have nonzero finite fourth moments;there is no perfect multicollinearity).In addition,there are two further assumptions,one of which is
(Multiple Choice)
4.9/5  (42)
(42)
For the OLS estimator  = (
= (  X)-1
X)-1  Y to exist,X'X must be invertible.This is the case when X has full rank.What is the rank of a matrix? What is the rank of the product of two matrices? Is it possible that X could have rank n? What would be the rank of X'X in the case n<(k+1)? Explain intuitively why the OLS estimator does not exist in that situation.
Y to exist,X'X must be invertible.This is the case when X has full rank.What is the rank of a matrix? What is the rank of the product of two matrices? Is it possible that X could have rank n? What would be the rank of X'X in the case n<(k+1)? Explain intuitively why the OLS estimator does not exist in that situation.
(Essay)
4.9/5  (38)
(38)
The Gauss-Markov theorem for multiple regression states that the OLS estimator
(Multiple Choice)
4.9/5  (40)
(40)
Write down,in general,the variance-covariance matrix for the multiple regression error term U.Using the assumptions cov(ui,uj|XiXj)= 0 and var(ui|Xi)=  .Show that the variance-covariance matrix can be written as
.Show that the variance-covariance matrix can be written as  In.
In.
(Essay)
4.8/5  (28)
(28)
Write the following three linear equations in matrix format Ax = b,where x is a 3×1 vector containing q,p,and y,A is a 3×3 matrix of coefficients,and b is a 3×1 vector of constants.
q = 5 +3 p - 2 y
q = 10 - p + 10 y
p = 6 y
(Essay)
4.9/5  (38)
(38)
The presence of correlated error terms creates problems for inference based on OLS.These can be overcome by
(Multiple Choice)
4.8/5  (37)
(37)
Showing 1 - 20 of 50
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)