Exam 16: Additional Topics in Time Series Regression
Some macroeconomic theories suggest that there is a short-run relationship between the inflation rate and the unemployment rate.How would you go about forecasting these two variables? Suggest various alternatives and discuss their advantages and disadvantages.
There are various methods available for forecasting the inflation rate and the unemployment rate.One basic distinction is whether or not the two variables are forecasted separately,or jointly as a system of two equations.Another distinction involves one period ahead forecasts vs.multiperiod forecasts.Finally,if multiperiod forecasts are used,then there is a multiperiod forecasting regression method vs.an interated forecast method.
Univariate Regression Methods: Here either the change in the inflation rate or the unemployment rate is modeled as an AR(p)and estimated by OLS.Observed values for the regressors are then substituted to produce a one period ahead forecast.(The one period ahead forecast for the inflation rate can then also be derived. )Statistical methods,such as the BIC or AIC can be used for choosing the number of lags.There are two important properties of the forecasts: the best forecast of either the change of the inflation rate or the unemployment rate depends only on the most recent p past values,and the errors are serially uncorrelated.These follow from the OLS assumptions.The multiperiod regression method for making an h-period ahead forecast of the change in inflation or unemployment rate using the AR(p)involves regressing these variables on its p lags,starting from (t-h),i.e. ,Yt = δ0 + δ1Yt-h + ...+ δpYt-p-h+1 + ut.Since the error term is serially correlated for the multiperiod regression,HAC standard errors must be used to have a reliable basis for inference.The iterated AR forecast method for the AR(p)is achieved by forecasting one period ahead initially,then using the forecasted value for the two period ahead forecast,and so on.More formally,the two-period ahead forecast is 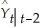 =
=  0 +
0 +  1
1 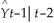 +
+  2Yt-2 +
2Yt-2 +  3Yt-3 + ...+
3Yt-3 + ...+  pYt-p,while the three-period ahead forecast is
pYt-p,while the three-period ahead forecast is  =
= 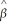 0 +
0 +  1
1 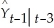 +
+ 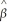 2Yt-2
2Yt-2  3 +
3 + 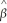 3Yt-3 + ...+
3Yt-3 + ...+  pYt-p,etc.
pYt-p,etc.
Multiple Predictors: If economic theory suggests that other variables could help forecast either the change in the inflation rate or the unemployment rate,then lags of these variables can be included.The Granger-causality test can be used to determine whether or not these additional variables belong in the regression.The same methods that were used for the AR(p)model can be applied for the ADL(p,q)model.For example,in the multiperiod forecasting using multivariate forecasts,all regressors must be lagged h periods to produce the h-period ahead forecast.To forecast both the change in the inflation and unemployment rate,regressions for each of the two dependent variables have to be estimated first,i.e. ,for both variables the following regression is estimated by OLS: Yt = δ0 + δ1Yt-h + ...+ δpYt-p-h + 1 + δp + 1Xt-h + ...+ δ2pXt-p-h + 1 + ut.Then the estimated coefficients are used to make the h-period ahead forecast.The interated forecast method now involves making one-period ahead forecasts using the estimated VAR specification,and using these forecasted values for both variables in subsequent forecasts.The two period ahead forecast,for example,for variables would be calculated as follows:  =
=  10 +
10 +  11
11  +
+  12 Yt-2 +
12 Yt-2 +  13Yt-3 + ...+
13Yt-3 + ...+ 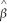 1pYt-p
1pYt-p
+  11
11 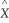 t-1
t-1  +
+ 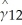 Xt-2 +
Xt-2 + 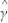 13Xt-3 + ...+
13Xt-3 + ...+  1pXt-p.
1pXt-p.
The decision on which method to use depends on the quality of the specification.If the AR(p)or the VAR is a good approximation to the underlying relationship,then the iterated forecast method is better.Note that if multiple predictors are involved,the ADL is not an alternative,since the additional predictors have to be forecasted themselves.However,even if one of the VAR equations is not a good representation of the underlying process,then the multiperiod regression forecasts are more accurate on average.Since the difference between the two methods is typically small,the textbook suggests to use the one "which is most conveniently implemented in your software."
The biggest conceptual difference between using VARs for forecasting and using them for structural modeling is that
B
Using the ADL(1,1)regression Yt = β0 + β1Yt-1 +  Xt-1 + ut,the ARCH model for the regression error assumes that ut is normally distributed with mean zero and variance
Xt-1 + ut,the ARCH model for the regression error assumes that ut is normally distributed with mean zero and variance  ,where
,where
The DOLS estimator has the following property if Xt and Yt are cointegrated:
In this case,the Granger causality statistic does not exceed the critical value,and hence the conclusion is that the change in the inflation rate does not Granger-cause the unemployment rate. 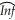 t = 0.05 - 0.31 ΔInft-1
(0.14)(0.07)
t = 1982:I - 2009:IV,R2 = 0.10,SER = 2.4
a.Calculate the one-quarter-ahead forecast of both ΔInf2010:I and Inf2010:I (the inflation rate in 2009:IV was 2.6 percent,and the change in the inflation rate for that quarter was -1.04).
b.Calculate the forecast for 2010:II using the iterated multiperiod AR forecast both for the change in the inflation rate and the inflation rate.
c.What alternative method could you have used to forecast two quarters ahead? Write down the equation for the two-period ahead forecast,using parameters instead of numerical coefficients,which you would have used.
t = 0.05 - 0.31 ΔInft-1
(0.14)(0.07)
t = 1982:I - 2009:IV,R2 = 0.10,SER = 2.4
a.Calculate the one-quarter-ahead forecast of both ΔInf2010:I and Inf2010:I (the inflation rate in 2009:IV was 2.6 percent,and the change in the inflation rate for that quarter was -1.04).
b.Calculate the forecast for 2010:II using the iterated multiperiod AR forecast both for the change in the inflation rate and the inflation rate.
c.What alternative method could you have used to forecast two quarters ahead? Write down the equation for the two-period ahead forecast,using parameters instead of numerical coefficients,which you would have used.
If Xt and Yt are cointegrated,then the OLS estimator of the coefficient in the cointegrating regression is
Consider the following model Yt = β0 + β1Xt + β2Xt-1 + β3Yt-1 + ut,where Xt is strictly exogenous.Show that by imposing the restriction  ,you can derive the following so-called Error Correction Mechanism (ECM)model
△Yt = β0 + β1△Xt - θ(Y - X)t-1 + ut
where θ = β1 + β2.What is the short-run (impact)response of a unit increase in X? What is the long-run solution? Why do you think the term in parenthesis in the above expression is called ECM?
,you can derive the following so-called Error Correction Mechanism (ECM)model
△Yt = β0 + β1△Xt - θ(Y - X)t-1 + ut
where θ = β1 + β2.What is the short-run (impact)response of a unit increase in X? What is the long-run solution? Why do you think the term in parenthesis in the above expression is called ECM?
The dynamic OLS (DOLS)estimator of the cointegrating coefficient,if Yt and Xt are cointegrated,
You have collected quarterly data for the unemployment rate (Unemp)in the United States,using a sample period from 1962:I (first quarter)to 2009:IV (the data is collected at a monthly frequency,but you have taken quarterly averages).
a.Does economic theory suggest that the unemployment rate should be stationary?
b.Testing the unemployment rate for stationarity,you run the following regression (where the lag length was determined using the BIC;using the AIC instead does not change the outcome of the test,even though it chooses 9 lags of the LHS variable):  t = 0.217 - 0.035 Unempt-1 + 0.689 ΔUnempt-1
(0.01)0.0012)(0.054)
Use the ADF statistic with an intercept only to test for stationarity.What is your decision?
c.The standard errors reported above were homoskedasticity-only standard errors.Do you think you could potentially improve on inference by allowing for HAC standard errors?
d.An alternative test for a unit root,the DF-GLS,produces a test statistic of -2.75.Find the critical value and decide whether or not to reject the null hypothesis.If the decision is different from (c),is there any reason why you might prefer the DF-GLS test over the ADF test?
t = 0.217 - 0.035 Unempt-1 + 0.689 ΔUnempt-1
(0.01)0.0012)(0.054)
Use the ADF statistic with an intercept only to test for stationarity.What is your decision?
c.The standard errors reported above were homoskedasticity-only standard errors.Do you think you could potentially improve on inference by allowing for HAC standard errors?
d.An alternative test for a unit root,the DF-GLS,produces a test statistic of -2.75.Find the critical value and decide whether or not to reject the null hypothesis.If the decision is different from (c),is there any reason why you might prefer the DF-GLS test over the ADF test?
You have collected time series for various macroeconomic variables to test if there is a single cointegrating relationship among multiple variables.Formulate the null hypothesis and compare the EG-ADF statistic to its critical value.
(a)Canadian unemployment rate,Canadian Inflation Rate,United States unemployment rate,United States inflation rate;t = (-3.374).
(b)Approval of United States presidents (Gallup poll),cyclical unemployment rate,inflation rate,Michigan Index of Consumer Sentiment;t = (-3.837).
(c)The log of real GDP,log of real government expenditures,log of real money supply (M2);t = (-2.23).
(d)Briefly explain how you could potentially improve on VAR(p)forecasts by using a cointegrating vector.
The following is not an appropriate way to tell whether two variables are cointegrated:
Consider the GARCH(1,1)model 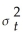 = α0 + α1
= α0 + α1 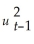 + φ1
+ φ1 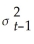 .Show that this model can be rewritten as
.Show that this model can be rewritten as 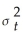 =
=  + α1(
+ α1( 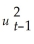 + φ1
+ φ1 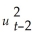 +
+ 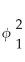
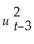 +
+ 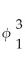
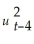 + ... ).(Hint: use the GARCH(1,1)model but specify it for
+ ... ).(Hint: use the GARCH(1,1)model but specify it for  ;substitute this expression into the original specification,and so on. )Explain intuitively the meaning of the resulting formulation.
;substitute this expression into the original specification,and so on. )Explain intuitively the meaning of the resulting formulation.
Your textbook states that there "are three ways to decide if two variables can plausibly be modeled as cointegrated: use expert knowledge and economic theory,graph the series and see whether they appear to have a common stochastic trend,and perform statistical tests for cointegration.All three ways should be used in practice." Accordingly you set out to check whether (the log of)consumption and (the log of)personal disposable income are cointegrated.You collect data for the sample period 1962:I to 1995:IV and plot the two variables. 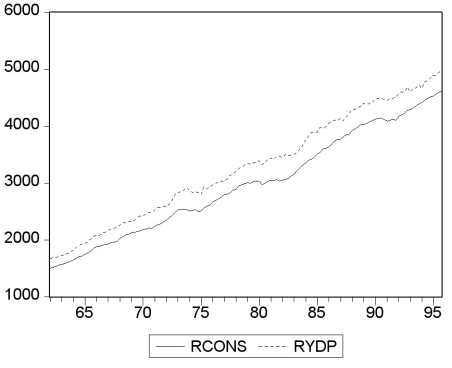 (a)Using the first two methods to examine the series for cointegration,what do you think the likely answer is?
(b)You begin your numerical analysis by testing for a stochastic trend in the variables,using an Augmented Dickey-Fuller test.The t-statistic for the coefficient of interest is as follows:
(a)Using the first two methods to examine the series for cointegration,what do you think the likely answer is?
(b)You begin your numerical analysis by testing for a stochastic trend in the variables,using an Augmented Dickey-Fuller test.The t-statistic for the coefficient of interest is as follows:
 where LnYpd is (the log of)personal disposable income,and LnC is (the log of)real consumption.The estimated equation included an intercept for the two growth rates,and,in addition,a deterministic trend for the level variables.For each case make a decision about the stationarity of the variables based on the critical value of the Augmented Dickey-Fuller test statistic.Why do you think a trend was included for level variables?
(c)Using the first step of the EG-ADF procedure,you get the following result:
where LnYpd is (the log of)personal disposable income,and LnC is (the log of)real consumption.The estimated equation included an intercept for the two growth rates,and,in addition,a deterministic trend for the level variables.For each case make a decision about the stationarity of the variables based on the critical value of the Augmented Dickey-Fuller test statistic.Why do you think a trend was included for level variables?
(c)Using the first step of the EG-ADF procedure,you get the following result:  t = -0.24 + 1.017 lnYpdt
Should you interpret this equation? Would you be impressed if you were told that the regression R2 was 0.998 and that the t-statistic for the slope was 266.06? Why or why not?
(d)The Dickey-Fuller test for the residuals for the cointegrating regressions results in a t-statistic of
(-3.64).State the null and alternative hypothesis and make a decision based on the result.
(e)You want to investigate if the slope of the cointegrating vector is one.To do so,you use the DOLS estimator and HAC standard errors.The slope coefficient is 1.024 with a standard error of 0.009.Can you reject the null hypothesis that the slope equals one?
t = -0.24 + 1.017 lnYpdt
Should you interpret this equation? Would you be impressed if you were told that the regression R2 was 0.998 and that the t-statistic for the slope was 266.06? Why or why not?
(d)The Dickey-Fuller test for the residuals for the cointegrating regressions results in a t-statistic of
(-3.64).State the null and alternative hypothesis and make a decision based on the result.
(e)You want to investigate if the slope of the cointegrating vector is one.To do so,you use the DOLS estimator and HAC standard errors.The slope coefficient is 1.024 with a standard error of 0.009.Can you reject the null hypothesis that the slope equals one?
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)