Explore all topics
Start Free Trial
Need Help? Contact us
back arrowfull exam logo
search
ai logoChat with AI
Servicesarrow
Discoverarrow

Topics

Explore all topics
Discover more topics

Exam 8: Nonlinear Regression Functions

arrow
Exam 1: Economic Questions and Data17 Questionsadd course
Exam 2: Review of Probability71 Questionsadd course
Exam 3: Review of Statistics63 Questionsadd course
Exam 4: Linear Regression With One Regressor65 Questionsadd course
Exam 5: Regression With a Single Regressor: Hypothesis Tests and Confidence Intervals59 Questionsadd course
Exam 6: Linear Regression With Multiple Regressors65 Questionsadd course
Exam 7: Hypothesis Tests and Confidence Intervals in Multiple Regression65 Questionsadd course
Exam 8: Nonlinear Regression Functions62 Questionsadd course
Exam 9: Assessing Studies Based on Multiple Regression65 Questionsadd course
Exam 10: Regression With Panel Data50 Questionsadd course
Exam 11: Regression With a Binary Dependent Variable50 Questionsadd course
Exam 12: Instrumental Variables Regression50 Questionsadd course
Exam 13: Experiments and Quasi-Experiments50 Questionsadd course
Exam 14: Introduction to Time Series Regression and Forecasting50 Questionsadd course
Exam 15: Estimation of Dynamic Causal Effects50 Questionsadd course
Exam 16: Additional Topics in Time Series Regression50 Questionsadd course
Exam 17: The Theory of Linear Regression With One Regressor49 Questionsadd course
Exam 18: The Theory of Multiple Regression50 Questionsadd course
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags
search iconSearch Question
flashcardsStudy Flashcards
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags

Consider the population regression of log earnings [Yi,where Yi = ln(Earningsi)] against two binary variables: whether a worker is married (D1i,where D1i=1 if the ith person is married)and the worker's gender (D2i,where D2i=1 if the ith person is female),and the product of the two binary variables Yi = β0 + β1D1i + β2D2i + β3(D1i×D2i)+ ui.The interaction term

(Multiple Choice)
4.7/5
(34)
Question 61

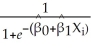Using a spreadsheet program such as Excel,plot the following logistic regression function with a single X, Using a spreadsheet program such as Excel,plot the following logistic regression function with a single X, i = ,where 0 = - 4.13 and 1 = 5.37.Enter values of X in the first column starting from 0 and then incrementing these by 0.1 until you reach 2.0.Then enter the logistic function formula in the next column.Finally produce a scatter plot,connecting the predicted values with a line. i = Using a spreadsheet program such as Excel,plot the following logistic regression function with a single X, i = ,where 0 = - 4.13 and 1 = 5.37.Enter values of X in the first column starting from 0 and then incrementing these by 0.1 until you reach 2.0.Then enter the logistic function formula in the next column.Finally produce a scatter plot,connecting the predicted values with a line. ,where Using a spreadsheet program such as Excel,plot the following logistic regression function with a single X, i = ,where 0 = - 4.13 and 1 = 5.37.Enter values of X in the first column starting from 0 and then incrementing these by 0.1 until you reach 2.0.Then enter the logistic function formula in the next column.Finally produce a scatter plot,connecting the predicted values with a line. 0 = - 4.13 and Using a spreadsheet program such as Excel,plot the following logistic regression function with a single X, i = ,where 0 = - 4.13 and 1 = 5.37.Enter values of X in the first column starting from 0 and then incrementing these by 0.1 until you reach 2.0.Then enter the logistic function formula in the next column.Finally produce a scatter plot,connecting the predicted values with a line. 1 = 5.37.Enter values of X in the first column starting from 0 and then incrementing these by 0.1 until you reach 2.0.Then enter the logistic function formula in the next column.Finally produce a scatter plot,connecting the predicted values with a line.

(Essay)
4.9/5
(46)
Question 62
Showing 61 - 62 of 62
close modal

Filters

  • Essay(0)
  • Multiple Choice(0)
  • Short Answer(0)
  • True False(0)
  • Matching(0)