Exam 22: Linear Programming
Exam 1: Operations and Productivity126 Questions
Exam 2: Operations Strategy in a Global Environment135 Questions
Exam 3: Project Management121 Questions
Exam 4: Forecasting144 Questions
Exam 5: Sustainability in the Supply Chain and Design of Goods and Services137 Questions
Exam 6: Managing Quality129 Questions
Exam 7: Process Strategy and Sustainability131 Questions
Exam 8: Location Strategies139 Questions
Exam 9: Layout Strategies161 Questions
Exam 10: Human Resources,job Design,and Work Measurement192 Questions
Exam 11: Supply-Chain Management145 Questions
Exam 12: Inventory Management168 Questions
Exam 13: Aggregate Planning134 Questions
Exam 14: Material Requirements Planning Mrpand ERP169 Questions
Exam 15: Short-Term Scheduling139 Questions
Exam 16: Jit and Lean Operations137 Questions
Exam 17: Maintenance and Reliability130 Questions
Exam 18: Statistical Process Control156 Questions
Exam 19: Capacity and Constraint Management107 Questions
Exam 20: Supply Chain Management Analytics55 Questions
Exam 21: Decision-Making Tools97 Questions
Exam 22: Linear Programming100 Questions
Exam 23: Transportation Models94 Questions
Exam 24: Waiting-Line Models135 Questions
Exam 25: Learning Curves111 Questions
Exam 26: Simulation92 Questions
Select questions type
A linear programming problem contains a restriction that reads "the quantity of X must be at least three times as large as the quantity of Y." Which of the following inequalities is the proper formulation of this constraint?
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
D
________ is a mathematical technique designed to help operations managers plan and make decisions relative to the trade-offs necessary to allocate resources.
Free
(Essay)
4.8/5  (35)
(35)
Correct Answer:
Linear programming
What combination of a and b will yield the optimum for this problem? Maximize $6a + $15b,subject to (1)4a + 2b < 12 and (2)5a + 2b < 20 and (3)a,b ≥ 0.
Free
(Multiple Choice)
4.9/5  (43)
(43)
Correct Answer:
C
Consider the following constraints from a two-variable linear program. (1)X ≥ 1
(2)Y ≥ 1
(3)X + Y ≤ 9
If these are the only constraints,which of the following points (X,Y)cannot be the optimal solution?
(Multiple Choice)
4.8/5  (35)
(35)
Phil Bert's Nuthouse is preparing a new product,a blend of mixed nuts.The product must be at most 50% peanuts,must have more almonds than cashews,and must be at least 10% pecans.The blend will be sold in one-pound bags.Phil's goal is to mix the nuts in such a manner that all conditions are satisfied and the cost per bag is minimized.Peanuts cost $1 per pound.Cashews cost $3 per pound.Almonds cost $5 per pound and pecans cost $6 per pound.Identify the decision variables of this problem.Write out the objective and the set of constraints for the problem.Do not solve.
(Essay)
4.7/5  (34)
(34)
Linear programming is an appropriate problem-solving technique for decisions that have no alternative courses of action.
(True/False)
4.7/5  (38)
(38)
Constraints are needed to solve linear programming problems by hand,but not by computer.
(True/False)
4.9/5  (35)
(35)
Linear programming helps operations managers make decisions necessary to make effective use of resources such as machinery,labour,money,time,and raw materials.
(True/False)
4.9/5  (43)
(43)
________ is an analysis that projects how much a solution might change if there were changes in the variables or input data.
(Essay)
4.9/5  (36)
(36)
For a linear programming problem with the constraints 2X + 4Y ≤ 100 and 1X + 8Y ≤ 100,two of its corner points are (0,0)and (0,25).
(True/False)
4.8/5  (37)
(37)
The property manager of a city government issues chairs,desks,and other office furniture to city buildings from a centralized distribution centre.Like most government agencies,it operates to minimize its costs of operations.In this distribution centre,there are two types of standard office chairs,Model A and Model B.Model A is considerably heavier than Model B,and costs $20 per chair to transport to any city building;each model B costs $14 to transport.The distribution centre has on hand 400 chairs-200 each of A and B.
The requirements for shipments to each of the city's buildings are as follows:
Building 1 needs at least 100 of A
Building 2 needs at least 150 of B.
Building 3 needs at least 100 chairs,but they can be of either type,mixed.
Building 4 needs 40 chairs,but at least as many B as A.
Write out the objective function and the constraints for this problem.(Hint: there are eight variables-chairs for building 1 cannot be used to satisfy the demands for another building).
(Essay)
4.9/5  (34)
(34)
A financial advisor is about to build an investment portfolio for a client who has $100,000 to invest.The four investments available are A,B,C,and D.Investment A will earn 4% and has a risk of two "points" per $1,000 invested.B earns 6% with 3 risk points;C earns 9% with 7 risk points;and D earns 11% with a risk of 8.The client has put the following conditions on the investments: A is to be no more than one-half of the total invested.A cannot be less than 20% of the total investment.D cannot be less than C.Total risk points must be at or below 1,000.Identify the decision variables of this problem.Write out the objective function and constraints.Do not solve.
(Essay)
4.8/5  (33)
(33)
A manager must decide on the mix of products to produce for the coming week.Product A requires three minutes per unit for molding,two minutes per unit for painting,and one minute for packing.Product B requires two minutes per unit for molding,four minutes for painting,and three minutes per unit for packing.There will be 600 minutes available for molding,600 minutes for painting,and 420 minutes for packing.Both products have contributions of $1.50 per unit.
a.Algebraically state the objective and constraints of this problem.
b.Plot the constraints on the grid below and identify the feasible region. 
(Essay)
4.8/5  (40)
(40)
The feasible region in the diagram below is consistent with which one of the following constraints? 
(Multiple Choice)
4.9/5  (32)
(32)
The region that satisfies the constraint 4X + 15Z ≥ 1000 includes the origin of the graph.
(True/False)
4.8/5  (45)
(45)
Solving a linear programming problem with the iso-profit line solution method requires that we move the iso-profit line to each corner of the feasible region until the optimum is identified.
(True/False)
4.8/5  (35)
(35)
A craftsman builds two kinds of birdhouses,one for wrens (X1),and one for bluebirds (X2).Each wren birdhouse takes four hours of labour and four units of lumber.Each bluebird house requires two hours of labour and twelve units of lumber.The craftsman has available 60 hours of labour and 120 units of lumber.Wren houses profit $6 each and bluebird houses profit $15 each.
Use the software output that follows to interpret the problem solution.Include a statement of the solution quantities (how many of which product),a statement of the maximum profit achieved by your product mix,and a statement of "resources unused" and "shadow prices." 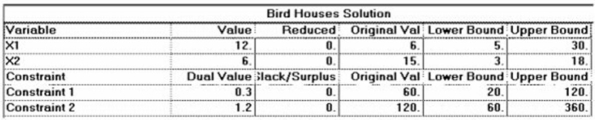
(Essay)
4.9/5  (33)
(33)
Showing 1 - 20 of 100
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)