Exam 26: Vehicle Routing and Scheduling
Exam 1: Operations and Productivity126 Questions
Exam 2: Operations Strategy in a Global Environment135 Questions
Exam 3: Project Management123 Questions
Exam 4: Forecasting142 Questions
Exam 5: Design of Goods and Services137 Questions
Exam 6: Managing Quality130 Questions
Exam 7: Process Strategy129 Questions
Exam 8: Location Strategies140 Questions
Exam 9: Layout Strategies161 Questions
Exam 10: Human Resources, Job Design, and Work Measurement191 Questions
Exam 11: Supply-Chain Management145 Questions
Exam 12: Inventory Management171 Questions
Exam 13: Aggregate Planning134 Questions
Exam 14: Material Requirements Planning Mrp and Erp172 Questions
Exam 15: Short-Term Scheduling139 Questions
Exam 16: Just-In-Time and Lean Options138 Questions
Exam 17: Maintenance and Reliability130 Questions
Exam 18: Statistical Tools for Managers97 Questions
Exam 19: Acceptance Sampling99 Questions
Exam 20: The Simplex Method of Linear Programming94 Questions
Exam 21: The Modi and Vam Methods of Solving Transportation Problems135 Questions
Exam 22: Vehicle Routing and Scheduling111 Questions
Exam 23 Managing Quality155 Questions
Exam 24: Process Strategy107 Questions
Exam 25: Supply-Chain Management73 Questions
Exam 26: Vehicle Routing and Scheduling92 Questions
Select questions type
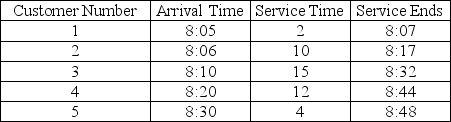
A waiting-line problem that cannot be modeled by standard distributions has been simulated. The table below shows the result of a Monte Carlo simulation. (Assume that the simulation began at 8:00 a.m. and there is only one server.) Why do you think this problem does not fit the standard distribution for waiting lines? Explain briefly how a Monte Carlo simulation might work where analytical models cannot.
Free
(Essay)
4.8/5  (30)
(30)
Correct Answer:
Service times do not appear to be exponential. Rather, they seem to be extreme-very short or very long. Simulation can handle this with a cumulative probability distribution and a set of random number intervals. The Monte Carlo simulation will, with a large enough number of trials, mimic the reality of this system.
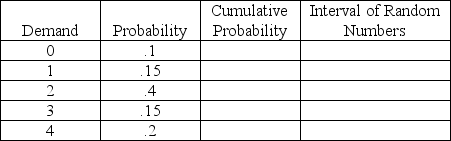
Complete the following table in preparation for a Monte Carlo simulation.
Free
(Essay)
4.8/5  (41)
(41)
Correct Answer:
One of the advantages of simulation is that
Free
(Multiple Choice)
5.0/5  (27)
(27)
Correct Answer:
C
From a portion of a probability distribution, you read that P(demand = 0) is 0.25, and P(demand = 1) is 0.30. The random number intervals for this distribution beginning with 01 are
(Multiple Choice)
4.9/5  (31)
(31)
The __________ method is a simulation technique that uses random elements when chance exists in their behavior.
(Short Answer)
4.9/5  (38)
(38)
In most real-world inventory problems, lead time and demand vary in ways that make simulation a necessity because mathematical modeling is extremely difficult.
(True/False)
5.0/5  (39)
(39)
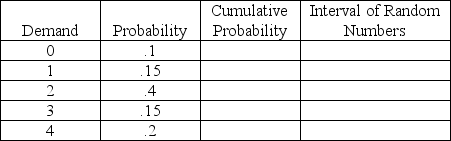
Create a distribution of random numbers that would result in average demand per period for a Monte Carlo simulation that is equivalent to the expected demand per period using the data given by the chart below.
(Essay)
4.9/5  (30)
(30)
A distribution of service times at a waiting line shows that service takes 6 minutes 30 percent of the time, 7 minutes 40 percent of the time, 8 minutes 20 percent of the time, and 9 minutes 10 percent of the time. This distribution has been prepared for Monte Carlo analysis. The first two random numbers drawn are 53 and 74. The simulated service times are __________ minutes, then __________ minutes.
(Multiple Choice)
4.9/5  (40)
(40)
Which of the following is a necessity for common EOQ methodology but not simulations
(Multiple Choice)
4.9/5  (42)
(42)
Simulation is the attempt to duplicate the features, appearance, and characteristics of a real system, usually by means of a computerized model.
(True/False)
4.9/5  (27)
(27)
Which of the following is true regarding the use of simulation?
(Multiple Choice)
4.8/5  (31)
(31)
Results of simulation experiments with large numbers of trials or long experimental runs will generally be better than those with fewer trials or shorter experimental runs.
(True/False)
4.8/5  (23)
(23)
What is the cumulative probability distribution of the following variable? 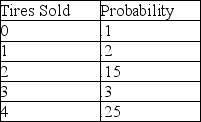
(Multiple Choice)
4.9/5  (30)
(30)
A simulation is "Monte Carlo" when the elements of a system being simulated exhibit chance in their behavior.
(True/False)
4.8/5  (39)
(39)
A small store is trying to determine if its current checkout system is adequate. Currently, there is only one cashier, so it is a single-channel, single-phase system. The store has collected information on the interarrival time, and service time distributions. They are represented in the tables below. Use the following two-digit random numbers given below to simulate 10 customers through the checkout system. What is the average time in line, and average time in system? (Set first arrival time to the interarrival time generated by first random number.
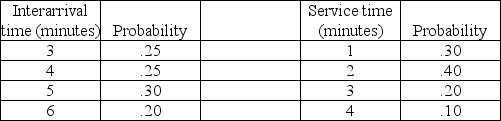 Random numbers for interarrival times: 07, 60, 77, 49, 76, 95, 51, 16, 14, 85
Random numbers of service times: 57, 17, 36, 72, 85, 31, 44, 30, 26, 09
Random numbers for interarrival times: 07, 60, 77, 49, 76, 95, 51, 16, 14, 85
Random numbers of service times: 57, 17, 36, 72, 85, 31, 44, 30, 26, 09
(Essay)
4.8/5  (35)
(35)
Showing 1 - 20 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)