Exam 26: Vehicle Routing and Scheduling
Exam 1: Operations and Productivity126 Questions
Exam 2: Operations Strategy in a Global Environment135 Questions
Exam 3: Project Management123 Questions
Exam 4: Forecasting142 Questions
Exam 5: Design of Goods and Services137 Questions
Exam 6: Managing Quality130 Questions
Exam 7: Process Strategy129 Questions
Exam 8: Location Strategies140 Questions
Exam 9: Layout Strategies161 Questions
Exam 10: Human Resources, Job Design, and Work Measurement191 Questions
Exam 11: Supply-Chain Management145 Questions
Exam 12: Inventory Management171 Questions
Exam 13: Aggregate Planning134 Questions
Exam 14: Material Requirements Planning Mrp and Erp172 Questions
Exam 15: Short-Term Scheduling139 Questions
Exam 16: Just-In-Time and Lean Options138 Questions
Exam 17: Maintenance and Reliability130 Questions
Exam 18: Statistical Tools for Managers97 Questions
Exam 19: Acceptance Sampling99 Questions
Exam 20: The Simplex Method of Linear Programming94 Questions
Exam 21: The Modi and Vam Methods of Solving Transportation Problems135 Questions
Exam 22: Vehicle Routing and Scheduling111 Questions
Exam 23 Managing Quality155 Questions
Exam 24: Process Strategy107 Questions
Exam 25: Supply-Chain Management73 Questions
Exam 26: Vehicle Routing and Scheduling92 Questions
Select questions type
A distribution of service times at a waiting line indicates that service takes 6 minutes 30 percent of the time, 7 minutes 40 percent of the time, 8 minutes 20 percent of the time, and 9 minutes 10 percent of the time. In preparing this distribution for Monte Carlo analysis, the service time 8 minutes would be represented by the random number range
(Multiple Choice)
4.8/5  (37)
(37)
A distribution of lead times in an inventory problem indicates that lead time was 1 day 20 percent of the time, 2 days 30 percent of the time, 3 days 30 percent of the time, and. 4 days 20 percent of the time. This distribution has been prepared for Monte Carlo analysis. The first four random numbers drawn are 06, 63, 57, and 02. The average lead time of this simulation is
(Multiple Choice)
4.7/5  (41)
(41)
Simulation models that are based on the generation of random numbers may fail to give the same solution in repeated use to any particular problem.
(True/False)
5.0/5  (34)
(34)
The numbers used to represent each possible value or outcome in a computer simulation are referred to as __________ .
(Short Answer)
4.9/5  (35)
(35)
Which of the following is not a step in running a Monte Carlo simulation?
(Multiple Choice)
4.8/5  (40)
(40)
The effects of OM policies over many months or years can be obtained by computer simulation in a short time. This phenomenon is referred to as
(Multiple Choice)
4.8/5  (25)
(25)
The idea behind simulation is threefold: (1) to imitate a real-world situation mathematically, (2) then to study its properties and operating characteristics, and (3) finally to draw conclusions and make action decisions based on the results of the simulation.
(True/False)
4.8/5  (34)
(34)
From a portion of a probability distribution, you read that P(demand = 0) is 0.05, P(demand = 1) is 0.10, and P(demand = 2) is 0.20. The two-digit random number intervals for this distribution beginning with 01 are
(Multiple Choice)
4.8/5  (36)
(36)
A distribution of service times at a waiting line indicates that service takes 12 minutes 30 percent of the time and 14 minutes 70 percent of the time. This distribution has been prepared for Monte Carlo analysis. The first four random numbers drawn are 07, 60, 77, and 49. The average service time of this simulation is
(Multiple Choice)
4.8/5  (27)
(27)
A distribution of service times at a waiting line indicates that service takes 12 minutes 30 percent of the time and 14 minutes 70 percent of the time. In preparing this distribution for Monte Carlo analysis, the service time 13 minutes would be represented by the random number range
(Multiple Choice)
4.9/5  (33)
(33)
From a portion of a probability distribution, you read that P(demand = 1) is 0.05, P(demand = 2) is 0.15, and P(demand = 3) is .20. The cumulative probability for demand 3 would be
(Multiple Choice)
4.9/5  (41)
(41)
A distribution of service times at a waiting line indicates that service takes 12 minutes 30 percent of the time and 14 minutes 70 percent of the time. Prepare the probability distribution, the cumulative probability distribution, and the random number intervals for this problem.
(Essay)
4.9/5  (37)
(37)
Julie's Diamond Boutique is very concerned with its order policies related to one-carat diamond solitaires. Their current policy is to order 10 diamonds whenever their inventory reaches 6 diamonds (unless there is already an ordered delivery due). Currently there are 8 diamonds on hand. Orders are placed at the end of the month and take one month to arrive . The following distribution of monthly sales has been developed using historical sales. If Julie's does not have a diamond on hand, it will result in a lost sale. Use the following random numbers to determine the number of lost sales of one-carat solitaires at Julie's over 12 months.
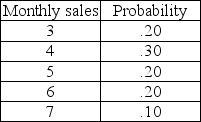 Random numbers for sales: 10, 24, 03, 32, 23, 59, 95, 34, 34, 51, 08, 48
Random numbers for sales: 10, 24, 03, 32, 23, 59, 95, 34, 34, 51, 08, 48
(Essay)
4.9/5  (33)
(33)
Explain what is meant by "simulation is not limited to using the standard probability distributions."
(Essay)
5.0/5  (37)
(37)
Sam's hardware store has an order policy of ordering 12 gallons of a specific primer whenever 7 gallons are on hand (unless there's already an ordered delivery due). The store would like to see how well their policy works. Assume that beginning inventory in period 1 is 10 units, that orders are placed at the end of the week to be received one week later. (In other words, if an order is placed at the end of week one, it is available at the beginning of week 3.) Assume that if inventory is not on hand, it will result in a lost sale. The weekly demand distribution obtained from past sales is found in the table below. Also, use the random numbers that are provided and simulate 10 weeks worth of sales. How many sales are lost?
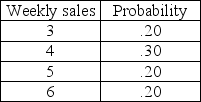 Random numbers for sales: 37, 60, 79, 21, 85, 71, 48, 39, 31, 35
Random numbers for sales: 37, 60, 79, 21, 85, 71, 48, 39, 31, 35
(Essay)
4.8/5  (33)
(33)
A warehouse manager needs to simulate the demand placed on a product that does not fit standard models. The concept being measured is "demand during lead time," where both lead time and daily demand are variable. The historical record for this product suggests the following probability distribution. Convert this distribution into random number intervals.
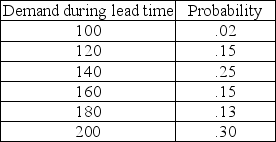
(Essay)
4.9/5  (41)
(41)
Showing 21 - 40 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)