Exam 14: Simple Linear Regression Analysis

An experiment was performed on a certain metal to determine if the strength is a function of heating time. The sample size consists of 10 metal sheets. Residuals are calculated for all 10 sheets and ordered from smallest to largest. Determine the normal point for the smallest residual.

The correlation coefficient may assume any value between

If one of the assumptions of the regression model is violated, performing data transformations on the ________ can remedy the situation.

Regression Analysis. 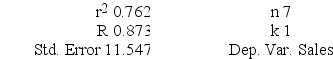ANOVA 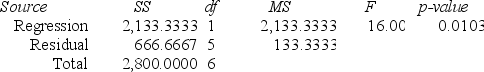Regression output A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model. What are the limits of the 99 percent prediction interval of the daily sales in dollars of an individual grocery store that has spent $3,000 on advertising expenditures? The distance value for this particular prediction is reported as .164.

A local tire dealer wants to predict the number of tires sold each month. He believes that the number of tires sold is a linear function of the amount of money invested in advertising. He randomly selects 6 months of data consisting of tire sales (in thousands of tires) and advertising expenditures (in thousands of dollars). Based on the data set with 6 observations, the simple linear regression model yielded the following results. ∑X = 24 ∑X² = 124 ∑Y = 42 ∑Y² = 338 ∑XY = 196 Calculate the standard error.

After plotting the data points on a scatter diagram, we have observed an inverse relationship between the independent variable (X) and the dependent variable (Y). Therefore, we can expect both the sample ________ and the sample ________ to be negative values.

The error term is the difference between an individual value of the dependent variable and the corresponding mean value of the dependent variable.

An experiment was performed on a certain metal to determine if the strength is a function of heating time. The sample size consists of 10 metal sheets. The simple linear regression equation is ŷ = 1 + 1X. The time is in minutes and the strength is measured in pounds per square inch. One of the 10 metal sheets was heated for 4 minutes and the resulting strength was 6 lb per square inch. Calculate the value of the residual for this observation.

In simple linear regression analysis, if the error terms exhibit a positive or negative autocorrelation over time, then the assumption of constant variance is violated.

Regression Analysis 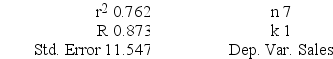ANOVA 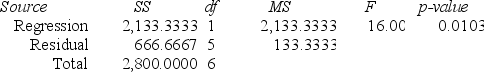Regression output A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model. What is the estimated simple linear regression equation?

The least squares point estimates of the simple linear regression model minimize the ________.

The ________ is the proportion of the total variation in the dependent variable explained by the regression model.

For a given data set, value of X, and confidence level, if all the other factors are constant, the confidence interval for the mean value of Y will ________ be wider than the corresponding prediction interval for the individual value of Y.

An experiment was performed on a certain metal to determine if the strength is a function of heating time. Results based on 10 metal sheets are given below. Use the simple linear regression model. ∑X = 30 ∑X² = 104 ∑Y = 40 ∑Y² = 178 ∑XY = 134 Calculate the 95 percent confidence interval for the slope.

The Durbin-Watson test statistic ranges from

A data set with 7 observations yielded the following. Use the simple linear regression model. ∑X = 21.57 ∑X² = 68.31 ∑Y = 188.9 ∑Y² = 5,140.23 ∑XY = 590.83 SSE = 1.117 Find the estimated y-intercept.

A significant positive correlation between X and Y implies that changes in X cause Y to change.

In a simple regression analysis for a given data set, if the null hypothesis β = 0 is rejected, then the null hypothesis ρ = 0 is also rejected. This statement is ________ true.

In a simple linear regression analysis, the correlation coefficient (a) and the slope (b) ________ have the same sign.

A local tire dealer wants to predict the number of tires sold each month. He believes that the number of tires sold is a linear function of the amount of money invested in advertising. He randomly selects 6 months of data consisting of monthly tire sales (in thousands of tires) and monthly advertising expenditures (in thousands of dollars). Residuals are calculated for all of the randomly selected six months and ordered from smallest to largest. Determine the normal score for the third residual in the ordered array.