Exam 14: Simple Linear Regression Analysis

A regression model was applied to a data set with 8 time-ordered observations. The residuals for these observations are given below. Calculate the Durbin-Watson statistic (d).

The ________ of the simple linear regression model is the value of y when the mean value of x is zero.

For the same set of observations on a specified dependent variable, two different independent variables were used to develop two separate simple linear regression models. A portion of the results is presented below. 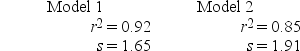Based on the results given above, we can conclude that

In simple regression analysis, r² is a percentage measure and measures the proportion of the variation explained by the simple linear regression model.

If there is significant autocorrelation present in a data set, the ________ assumption is violated.

Consider the following partial computer output from a simple linear regression analysis. 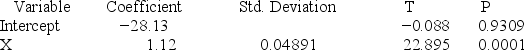R².9722 What is the estimated y-intercept?

Use the following results obtained from a simple linear regression analysis with 12 observations. = 37.2895 − (1.2024)X r² = .6744s_b = .2934 Test to determine if there is a significant negative relationship between the independent and dependent variables at α = .05. Give the test statistic and the resulting conclusion.

The ________ assumption requires that all variation around the regression line should be equal at all possible values (levels) of the ________variable.

Regression Analysis. ANOVA 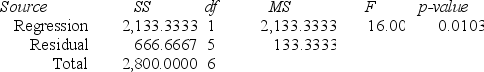Regression output A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model. Determine a 95 percent confidence interval estimate of the daily average store sales based on $3,000 advertising expenditures. The distance value for this particular prediction is reported as .164.

Based on 30 time-ordered observations from a simple regression, we have determined the Durbin-Watson statistic, d = 2.71. At α = .05, test to determine if there is any evidence of negative autocorrelation. State your conclusions.

Consider the following partial computer output from a simple linear regression analysis. 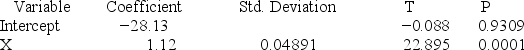R².9722 What is the predicted value of y when x = 1,000?

When the constant variance assumption holds, a plot of the residual versus x

Consider the following partial computer output from a simple linear regression analysis. S = .4862R-Sq = ________ Analysis of Variance What is the correlation coefficient?

A simple regression analysis with 20 observations would yield ________ degrees of freedom error and ________degrees of freedom total.

The ________ the r² and the ________ the s (standard error), the stronger the relationship between the dependent variable and the independent variable.

An experiment was performed on a certain metal to determine if the strength is a function of heating time. Results based on 10 metal sheets are given below. Use the simple linear regression model. ∑X = 30 ∑X² = 104 ∑Y = 40 ∑Y² = 178 ∑XY = 134 Calculate the correlation coefficient.

The dependent variable is the variable that is being described or predicted.

The least squares simple linear regression line minimizes the sum of the vertical deviations between the line and the data points.

A local tire dealer wants to predict the number of tires sold each month. He believes that the number of tires sold is a linear function of the amount of money invested in advertising. He randomly selects 6 months of data consisting of monthly tire sales (in thousands of tires) and monthly advertising expenditures (in thousands of dollars). The simple linear regression equation is ŷ = 3 + 1x, and the sample correlation coefficient (r²) = .6364. Test to determine if there is a significant correlation between the monthly tire sales and monthly advertising expenditures. Use H₀: ρ = 0 vs. H_A: ρ ≠ 0 at α = .05.

When using simple linear regression, we would like to use confidence intervals for the ________ and prediction intervals for the ________ at a given value of x.