Exam 8: Confidence Interval Estimation
Exam 1: Introduction to Business Analytics29 Questions
Exam 2: Describing the Distribution of a Single Variable100 Questions
Exam 3: Finding Relationships Among Variables85 Questions
Exam 4: Probability and Probability Distributions114 Questions
Exam 5: Normal, Binomial, Poisson, and Exponential Distributions125 Questions
Exam 6: Decision Making Under Uncertainty107 Questions
Exam 7: Sampling and Sampling Distributions90 Questions
Exam 8: Confidence Interval Estimation84 Questions
Exam 9: Hypothesis Testing87 Questions
Exam 10: Regression Analysis: Estimating Relationships92 Questions
Exam 11: Regression Analysis: Statistical Inference82 Questions
Exam 12: Time Series Analysis and Forecasting106 Questions
Exam 13: Introduction to Optimization Modeling97 Questions
Exam 14: Optimization Models114 Questions
Exam 15: Introduction to Simulation Modeling82 Questions
Exam 16: Simulation Models102 Questions
Exam 17: Data Mining20 Questions
Exam 18: Importing Data Into Excel19 Questions
Exam 19: Analysis of Variance and Experimental Design20 Questions
Exam 20: Statistical Process Control20 Questions
Select questions type
As a general rule, the normal distribution is used to approximate the sampling distribution of the sample proportion 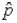 only if the sample size n is greater than 30.
only if the sample size n is greater than 30.
(True/False)
4.8/5  (39)
(39)
In general, the paired-sample procedure is appropriate when the samples are naturally paired in some way and there is a reasonably large positive correlation between the pairs. In this case, the paired-sample procedure makes more efficient use of the data and generally results in narrower confidence intervals.
(True/False)
4.9/5  (39)
(39)
The mean of the sampling distribution of the sample proportion 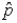 , when the sample size n = 100 and the population proportion p = 0.15, is 15.0.
, when the sample size n = 100 and the population proportion p = 0.15, is 15.0.
(True/False)
4.7/5  (36)
(36)
(A) Construct a 90% confidence interval estimate of the mean family dental expenses for all employees of this corporation.
(B) What assumption about the population distribution must be made to answer (A)?
(C) Interpret the 90% confidence interval constructed in (A).
(D) Suppose you used a 95% confidence interval in (A). What would be your answer?
(E) Suppose the fourth value were 593 instead of 93. What would be your answer to (A)? What effect does this change have on the confidence interval?
(F) Construct a 90% confidence interval estimate for the standard deviation of family dental expenses for all employees of this corporation.
(G) Interpret the 90% confidence interval constructed in (E).
(Essay)
4.8/5  (42)
(42)
The degrees of freedom for the t and chi-square distributions is a numerical parameter of the distribution that defines the precise shape of the distribution.
(True/False)
4.9/5  (49)
(49)
The 95% confidence interval for the population mean 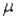 , given that the sample size n = 49 and the population standard deviation
, given that the sample size n = 49 and the population standard deviation 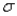 = 7, is
= 7, is 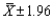 .
.
(True/False)
4.8/5  (38)
(38)
In determining the sample size n for estimating the population proportion p, a conservative value of n can be obtained by using 0.50 as an estimate of p.
(True/False)
4.9/5  (35)
(35)
If two random samples of sizes 30 and 35 are selected independently from two populations whose means are 85 and 90, then the mean of the sampling distribution of the sample mean difference, 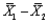 , equals 5.
, equals 5.
(True/False)
4.9/5  (46)
(46)
In developing a confidence interval for the population standard deviation 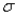 , we make use of the fact that the sampling distribution of the sample standard deviation s is not the normal distribution or the t-distribution, but rather a right-skewed distribution called the chi-square distribution, which (for this procedure) has n - 1 degrees of freedom.
, we make use of the fact that the sampling distribution of the sample standard deviation s is not the normal distribution or the t-distribution, but rather a right-skewed distribution called the chi-square distribution, which (for this procedure) has n - 1 degrees of freedom.
(True/False)
4.8/5  (30)
(30)
In past years, approximately 25% of all U.S. families purchased potato chips at least once a month. We are interested in determining the fraction of all U.S. families that currently purchase potato chips at least once a month. How many families must we survey if we want to be 99% sure that our estimate of the fraction of U.S. families currently purchasing potato chips at least once a month is accurate within 2%?
(Essay)
4.8/5  (32)
(32)
The chi-square and F-distributions are used primarily to make inferences about population ____.
(Multiple Choice)
4.9/5  (43)
(43)
A confidence interval is an interval that, with a stated level of confidence, captures a population parameter.
(True/False)
4.8/5  (38)
(38)
Two independent samples of sizes 20 and 25 are randomly selected from two normal populations with equal variances. In order to test the difference between the population means, the test statistic is:
(Multiple Choice)
4.9/5  (42)
(42)
(A) Construct a 99% confidence interval for the standard deviation of the number of hours this firm's employees spend on work-related activities in a typical week.
(B) Interpret the 99% confidence interval constructed in (A).
(C) Given the target range of 40 to 60 hours of work per week, should senior management be concerned about the number of hours their employees are currently devoting to work? Explain why or why not.
(Essay)
4.8/5  (31)
(31)
Q-Mart is interested in comparing customers who use its own charge card with those who use other types of credit cards. Q-Mart would like to know if customers who use the Q-Mart card spend more money per visit, on average, than customers who use some other type of credit cards. They have collected information on a random sample of 38 charge customers as shown below. On average, the person using a Q-Mart card spends $192.81 per visit and customers using another type of card spend $104.47 per visit. 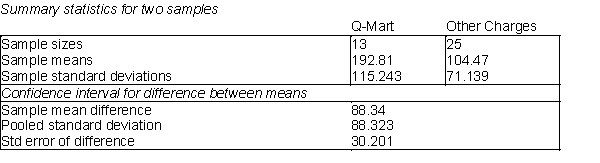 -(A) Using a t - value of 2.0281, calculate a 95% confidence interval for the difference between the average Q-Mart charge and the average charge on another type of credit card.
(B) What are the degrees of freedom for the t - multiple in this calculation? Explain how you would calculate the degrees of freedom in this case.
(C) What is the assumption in this case that allows you to use the pooled standard deviation for this confidence interval?
(D) Would you conclude that there is a significant difference between the two types of customers in this case? Explain.
-(A) Using a t - value of 2.0281, calculate a 95% confidence interval for the difference between the average Q-Mart charge and the average charge on another type of credit card.
(B) What are the degrees of freedom for the t - multiple in this calculation? Explain how you would calculate the degrees of freedom in this case.
(C) What is the assumption in this case that allows you to use the pooled standard deviation for this confidence interval?
(D) Would you conclude that there is a significant difference between the two types of customers in this case? Explain.
(Essay)
4.8/5  (39)
(39)
The confidence interval for the population standard deviation σ is centered at the point estimate, the sample standard deviation s.
(True/False)
4.8/5  (39)
(39)
The following values have been calculated using the T DIST and T INV functions in Excel®. These values come from a t- distribution with 15 degrees of freedom.
These values represent the probability to the right of the given positive values.  These values represent the positive t- value for a given probability in both tails (sum of both tails).
These values represent the positive t- value for a given probability in both tails (sum of both tails).  -What is the probability of a t-value between -1.40 and +1.40?
-What is the probability of a t-value between -1.40 and +1.40?
(Short Answer)
4.8/5  (35)
(35)
(A) Construct a 95% confidence interval estimate of the population proportion of all customers who still own the cars they purchased six years ago.
(B) How can the result in (A) be used by the automobile dealer to study satisfaction with cars purchased at the dealership?
(Essay)
4.8/5  (33)
(33)
The number of degrees of freedom needed to construct 90% confidence interval for the difference between means when the data are gathered from paired samples, with 15 observations in each sample, is:
(Multiple Choice)
4.9/5  (43)
(43)
Two independent samples of sizes 50 and 50 are randomly selected from two populations to test the difference between the population means, 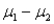 . The sampling distribution of the sample mean difference
. The sampling distribution of the sample mean difference 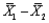 is:
is:
(Multiple Choice)
4.9/5  (36)
(36)
Showing 61 - 80 of 84
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)