Exam 5: Normal, Binomial, Poisson, and Exponential Distributions
Exam 1: Introduction to Business Analytics29 Questions
Exam 2: Describing the Distribution of a Single Variable100 Questions
Exam 3: Finding Relationships Among Variables85 Questions
Exam 4: Probability and Probability Distributions114 Questions
Exam 5: Normal, Binomial, Poisson, and Exponential Distributions125 Questions
Exam 6: Decision Making Under Uncertainty107 Questions
Exam 7: Sampling and Sampling Distributions90 Questions
Exam 8: Confidence Interval Estimation84 Questions
Exam 9: Hypothesis Testing87 Questions
Exam 10: Regression Analysis: Estimating Relationships92 Questions
Exam 11: Regression Analysis: Statistical Inference82 Questions
Exam 12: Time Series Analysis and Forecasting106 Questions
Exam 13: Introduction to Optimization Modeling97 Questions
Exam 14: Optimization Models114 Questions
Exam 15: Introduction to Simulation Modeling82 Questions
Exam 16: Simulation Models102 Questions
Exam 17: Data Mining20 Questions
Exam 18: Importing Data Into Excel19 Questions
Exam 19: Analysis of Variance and Experimental Design20 Questions
Exam 20: Statistical Process Control20 Questions
Select questions type
Let Y be the number of the 12 male adults who are less than 62 inches tall. Determine the mean and standard deviation of Y.
(Essay)
4.8/5  (33)
(33)
Given that Z is a standard normal random variable, P(-1.0 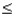 Z
Z 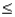 1.5) is:
1.5) is:
(Multiple Choice)
4.8/5  (40)
(40)
Find the probability that the number of arrivals between 4:00 and 5:00 P.M. is exactly two.
(Essay)
4.8/5  (41)
(41)
The public school system is interested in examining the probability of a child being late to school. The child is categorized as either late or not late. What type of distribution should the school use to examine this issue?
(Multiple Choice)
4.7/5  (40)
(40)
Find the probability that the number of arrivals between 3:30 and 4:00 P.M. is at least 10.
(Essay)
4.7/5  (32)
(32)
A random variable X is normally distributed with a mean of 175 and a standard deviation of 50. Given that X = 150, its corresponding Z- score is -0.50.
(True/False)
4.9/5  (40)
(40)
If the random variable X is exponentially distributed with parameter 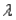 = 3, then P(X
= 3, then P(X 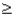 2) , up to 4 decimal places, is:
2) , up to 4 decimal places, is:
(Multiple Choice)
4.9/5  (30)
(30)
What is the probability that at least one of the 20 new microwaves sold will require a warranty repair in the first 90 days?
(Short Answer)
4.7/5  (31)
(31)
What is the probability that at least 20 customers, but fewer than 30 customers arrive at this checkout counter in a given hour?
(Short Answer)
4.8/5  (42)
(42)
Given that the random variable X is normally distributed with a mean of 80 and a standard deviation of 10, P(85 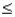 X
X 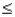 90) is:
90) is:
(Multiple Choice)
4.8/5  (31)
(31)
Which distribution is best-suited to measure the length of time between arrivals at a grocery checkout counter?
(Multiple Choice)
4.9/5  (32)
(32)
What is the probability that exactly half the male adults will be less than 62 inches tall?
(Essay)
4.8/5  (33)
(33)
Which probability distribution applies to the number of events occurring within a specified period of time or space?
(Multiple Choice)
4.8/5  (28)
(28)
Using the standard normal curve, the Z- score representing the 10th percentile is 1.28.
(True/False)
4.8/5  (28)
(28)
What is the variance of the time it takes a technician to fix a computer problem?
(Short Answer)
4.9/5  (39)
(39)
What is the probability that at most two of the 20 new microwaves sold will require a warranty repair in the first 90 days?
(Short Answer)
4.9/5  (22)
(22)
Showing 21 - 40 of 125
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)