Exam 5: Normal, Binomial, Poisson, and Exponential Distributions

What is the probability that it will take a technician less than 10 minutes to fix a computer problem?

What two dollar amounts, equidistant from the mean of $30, such that 90% of all customer purchases are between these values?

What is the probability that the number of customers who arrive at this checkout counter in a given hour will be greater than 35?

What percentage of students scored between 81 and 89 on this exam?

Using the standard normal distribution, the Z- score representing the 99th percentile is 2.326.

The Poisson distribution is characterized by a single parameter 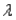, which must be positive.

What is the probability that at least 25 customers arrive at this checkout counter in a given hour?

Which of the following might not be appropriately modeled with a normal distribution?

If the random variable X is exponentially distributed with parameter 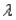= 1.5, then P(2 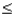X 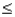4), up to 4 decimal places, is:

A continuous random variable X has the probability density function: f(x) = 2 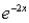, 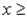0 -What is the probability that X is at most 2?

Describe the probability distribution of X.

Find P(X < 3).

What number of cars, equidistant from the mean, such that 98% of car sales are between these values?

The library is interested in estimating the number of individuals who use the computers during the lunch hour. Which probability distribution should they use?

What is the probability that the number of customers who arrive at this checkout counter in a given hour will be between 30 and 35 (inclusive)?

If the random variable X is normally distributed with mean 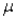and standard deviation 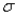, then the random variable Z defined by 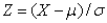is also normally distributed with mean 0 and standard deviation 1.

For a given probability of success p that is not too close to 0 or 1, the binomial distribution tends to take on more of a symmetric bell shape as the number of trials n increases.

(A) Using the binomial distribution, find the probability that 6 or more of the 30 students taking this course in a given semester will withdraw from the class. (B) Using the normal approximation to the binomial, find the probability that 6 or more of the 30 students taking this course in a given semester will withdraw from the class. (C) Compare the results obtained in (A) and (B). Under what conditions will the normal approximation to this binomial probability become even more accurate?

What two dollar amounts, equidistant from the mean of $30, such that 98% of all customer purchases are between these values?

Calculate the mean, variance, and standard deviation for the entire year (assume 52 weeks in the year).