Exam 21: Decision Analysis on Website

Exhibit 21-5 Below you are given a payoff table involving three states of nature and three decision alternatives. The probability of occurrence of S₁ is 0.2 and the probability of occurrence of S₂ is 0.3. -Refer to Exhibit 21-5. The expected monetary value of the best alternative is

Exhibit 21-4 Below you are given a payoff table involving two states of nature and three decision alternatives. The probability of the occurrence of S₁ = 0.3. -Refer to Exhibit 21-4. The expected value of the best alternative is

A line or arc connecting the nodes of a decision tree is called a(n)

In computing an expected value (EV), the weights are

Exhibit 21-4 Below you are given a payoff table involving two states of nature and three decision alternatives. The probability of the occurrence of S₁ = 0.3. -Refer to Exhibit 21-4. The recommended decision alternative based on the expected monetary value is

Exhibit 21-1 Below you are given a payoff table involving two states of nature and three decision alternatives. The probability of occurrence of S₁ = 0.2. -Refer to Exhibit 21-1. The recommended decision alternative based on the expected monetary value is

The difference between the expected value of an optimal strategy based on sample information and the "best" expected value without any sample information is called the

Suppose we are interested in investing in one of three investment opportunities: d₁, d₂, or d₃. The following profit payoff table shows the profits (in thousands of dollars) under each of the 3 possible economic conditions-S₁, S₂, and S₃. Assume the states of nature have the following probabilities of occurrence.P(S₁) = 0.2 P(S₂) = 0.3 P(S₃) = 0.5 a.Determine the expected value of each alternative and indicate which decision alternative is the best. b.Determine the expected value with perfect information about the states of nature. c.Determine the expected value of perfect information.

Assume you are faced with the following decision alternatives and two states of nature. The probability of the occurrence of state of nature 1 is 0.35. The payoff table is shown below. a.Determine the expected value of each alternative and indicate which decision alternative is the best. b.Determine the expected value with perfect information about the states of nature. c.Determine the expected value of perfect information.

Exhibit 21-2 Below you are given a payoff table involving three states of nature and two decision alternatives. The probability that S₁ will occur is 0.1; the probability that S₂ will occur is 0.6. -Refer to Exhibit 21-2. The expected value of the best alternative equals

A group of investors wants to open up a jewelry store in a new shopping center. The investors are trying to decide whether to stock the store with inexpensive jewelry, medium-priced jewelry, or expensive jewelry. The probability of their choice depends upon the economic conditions. The payoff table below gives the anticipated profits for different states of the economy. The probability of prosperity is 0.5. 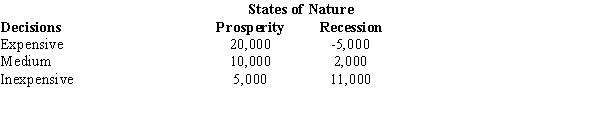a.Determine the expected value of each alternative and indicate which decision alternative is the best. b.Determine the expected value with perfect information about the states of nature. c.Determine the expected value of perfect information.

You are given the following payoff table. Assume the following probability information is given. 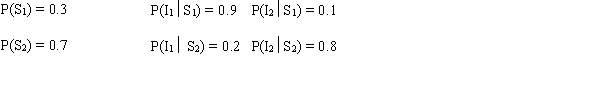a.Find the values of P(I₁) and P(I₂). b.What are the values of P(S₁ $\mid$ I₁), P(S₂ $\mid$ I₁), P(S₁ $\mid$ I₂), and P(S₂ $\mid$ I₂)? c.Use the decision tree approach and determine the optimal decision strategy. What is the expected value of the solution? d.Determine the expected value of sample information.

Exhibit 21-4 Below you are given a payoff table involving two states of nature and three decision alternatives. The probability of the occurrence of S₁ = 0.3. -Refer to Exhibit 21-4. The expected value of perfect information is

Exhibit 21-5 Below you are given a payoff table involving three states of nature and three decision alternatives. The probability of occurrence of S₁ is 0.2 and the probability of occurrence of S₂ is 0.3. -Refer to Exhibit 21-5. The recommended decision alternative based on the expected monetary value is

The owner of a new gourmet kitchenware shop wishes to determine how many days and evenings to keep the shop open. The various payoffs (in $1,000s) are indicated in the table below. 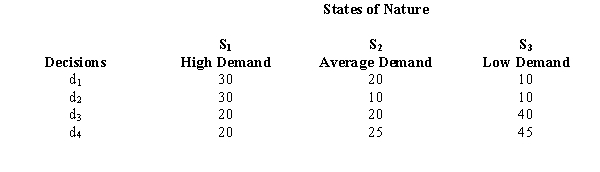Assume the probabilities of the three states of nature are P(S₁) = 0.60, P(S₂) =0 .30, and P(S₃) = 0.1. a.Determine the expected value of each alternative and indicate which decision alternative is the best. b.Determine the expected value with perfect information about the states of nature. c.Determine the expected value of perfect information.

An uncertain future event affecting the consequence, or payoff, associated with a decision is known as

New information obtained through research or experimentation that enables an updating or revision of the state-of-nature probabilities is

Michael, Nancy, & Associates (MNA) produce color printers. The demand for their printers could be light, medium, or high with the following probabilities. The company has three production alternatives for the coming period. The payoffs (in millions of dollars) associated with the three alternatives are shown below. a.Compute the expected value of the three alternatives. Which alternative would you select, based on the expected values? b.Compute the expected value with perfect information (i.e., expected value under certainty). c.Compute the expected value of perfect information (EVPI).

You are given a decision situation with three possible states of nature S₁, S₂, and S₃. The prior probabilities of the three states are 0.20, 0.45, and 0.35. With sample information I, you are provided with the following information. P(I₁ $\mid$ S₁) = 0.85 P(I₁ $\mid$ ₂) = 0.70 P(I₁ $\mid$ S₃) = 0.40 a.Compute P(I). b.Compute the revised probabilities of P(S₁ $\mid$ I), P(S₂ $\mid$ I), and P(S₃ $\mid$ I).

The efficiency of information is the ratio of