Exam 21: Decision Analysis on Website

A poll released this week found that in a random sample of registered voters, 60% indicated that they think a female "will run" for the presidency, 30% said a female "will not run," and 10% had "no opinion." When asked their opinions on whether or not a female would be elected, 66% of those who said a female "will run" thought she could be elected; 25% of those who thought a female "will not run" thought she could be elected; whereas, 20% of those who had no opinion said that she could be elected. a.What percentage of registered voters (in this sample) thought that a female could be elected? b.Given that a person thought that a female could be elected, what is the probability that this person said a female "will not run" for the presidency? c.Compute all the posterior probabilities.

The uncontrollable future events that can affect the outcome of a decision are known as

Assume you have a sum of money available that you would like to invest in one of the two available investment plans: stocks or bonds. The conditional payoffs of each plan under two possible economic conditions are as follows. 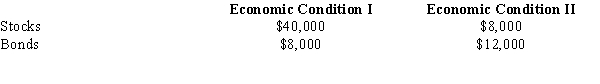a.If the probability of Economic Condition I occurring is 0.8, where should you invest your money? Use the expected monetary value criterion and show your complete work. b.Compute the expected value with perfect information about the economic conditions (expected value under certainty). c.Determine expected value of perfect information (EVPI).

The probability of one event given the known outcome of a (possibly) related event is known as

Exhibit 21-2 Below you are given a payoff table involving three states of nature and two decision alternatives. The probability that S₁ will occur is 0.1; the probability that S₂ will occur is 0.6. -Refer to Exhibit 21-2. The recommended decision based on the expected value criterion is

You are given the following payoff table. 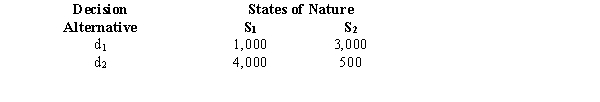Assume the following probability information is given. P(S₁) = 0.45 P(I₁ $\mid$ S₁) = 0.7 P(I₂ $\mid$ S₁) = 0.3 P(S₂) = 0.55 P(I₁ $\mid$ S₂) = 0.6 P(I₂ $\mid$ S₂) = 0.4 a.Find the values of P(I₁) and P(I₂). b.Determine the values of P(S₁ $\mid$ I₁), P(S₂ $\mid$ I₁), P(S₁ $\mid$ I₂), and P(S₂ $\mid$ I₂). c.Use the decision tree approach and determine the optimal strategy. What is the expected value of your solution?

Exhibit 21-3 Below you are given a payoff table involving two states of nature and three decision alternatives. The probability of the occurrence of state of nature S₁ is 0.4. -Refer to Exhibit 21-3. The recommended decision based on the expected monetary value criterion is

The Video Game Supply Company (VGS) is deciding whether to set production next year at 2,000, 2,500, or 3,000 games. Demand could be low, medium, or high. Using historical data, VGS estimates the probabilities as 0.4 for low demand, 0.3 for medium demand, and 0.3 for high demand. The following profit payoff table (in $100s) has been developed. 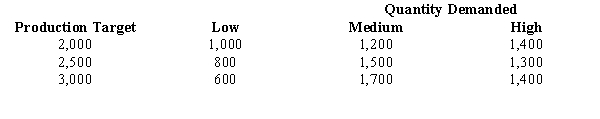a.Determine the expected value of each alternative and indicate what should be the production target. b.Determine the expected value with perfect information about the states of nature. c.Determine the expected value of perfect information.

An intersection or junction point of a decision tree is called a (n)

The expected value of information that would tell the decision maker exactly which state of nature is going to occur is

The following payoff table shows profits for two decision alternatives under three different states of nature. It is known that the probability of the occurrence of state of nature 1 is 0.1. a.What should the probabilities of states of natures 2 and 3 be so that the expected values of the two decision alternatives equal one another? b.Determine the expected values.

Exhibit 21-4 Below you are given a payoff table involving two states of nature and three decision alternatives. The probability of the occurrence of S₁ = 0.3. -Refer to Exhibit 21-4. The expected monetary value of alternative C is

An investor has a choice between four investments. The profitability of the investments depends upon the market. The payoff table is given below for different market conditions. 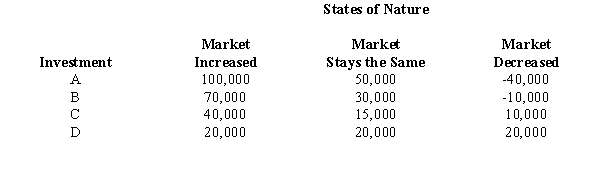a.A market economist has stated that there is a 25% chance that the market will stay the same, a 35% chance that the market will decrease, and a 40% chance that the market will increase. Compute the expected monetary value for each investment. Which investment is the best? b.Compute the expected value of perfect information.

Future events that cannot be controlled by the decision maker are called

A graphic presentation of the expected gain from the various options open to the decision maker is called

Suppose we are interested in investing in one of three investment opportunities: d₁, d₂, or d₃. The following profit payoff table shows the profits (in thousands of dollars) under each of the 3 possible economic conditions-S₁, S₂, and S₃. The probability of the occurrence of S₁ is 0.1, and the probability of the occurrence of S₂ is 0.3. a.Determine the expected value of each alternative and indicate which decision alternative is the best. b.Determine the expected value with perfect information about the states of nature. c.Determine the expected value of perfect information.

Assume you are faced with the following decision alternatives and two states of nature. The payoff table is shown below. Assume the states of nature have the following probabilities. P(S₁) = 0.4 P(S₂) = 0.6 a.Determine the expected value of each alternative and indicate which decision alternative is the best. b.Determine the expected value of perfect information.

Nodes indicating points where a decision is made are known as

Below you are given a payoff table involving two states of nature and two decision alternatives. 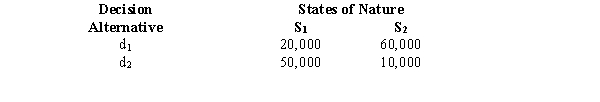The probability of the occurrence of S₁ is 0.3. a.Compute the expected monetary value for each decision. Which decision is the best? b.Compute the expected value of perfect information.

A decision criterion which weights the payoff for each decision by its probability of occurrence is known as the