Exam 1: Functions and Their Graphs
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Match the graph to the function listed whose graph most resembles the one given.
-
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-The gravitational attraction A between two masses varies inversely as the square of the distance between them. The force of attraction is 9 lb when the masses are 2 ft apart, what is the attraction when the masses are 6 ft
Apart?
(Multiple Choice)
4.9/5  (36)
(36)
Suppose the point (2, 4) is on the graph of y = f(x). Find a point on the graph of the given function.
-The reflection of the graph of y = f(x) across the y-axis
(Multiple Choice)
4.9/5  (39)
(39)
Answer the question about the given function.
-Given the function , what is the domain of ?
(Multiple Choice)
4.9/5  (31)
(31)
The graph of a function is given. Determine whether the function is increasing, decreasing, or constant on the given
interval.
-
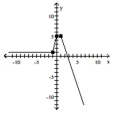
(Multiple Choice)
5.0/5  (34)
(34)
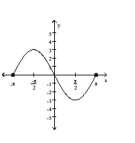
The graph of a function is given. Decide whether it is even, odd, or neither.
-
(Multiple Choice)
4.8/5  (32)
(32)
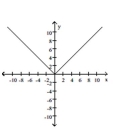
The graph of a function is given. Decide whether it is even, odd, or neither.
-
(Multiple Choice)
4.9/5  (31)
(31)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
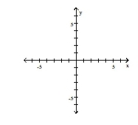 A)
A)
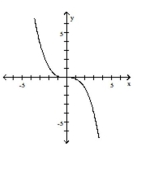 B)
B)
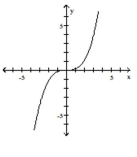 C)
C)
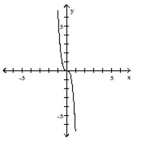 D)
D)
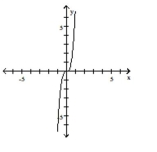
(Multiple Choice)
4.9/5  (32)
(32)
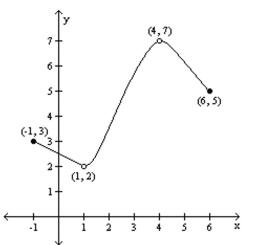
For the graph of the function y = f(x), find the absolute maximum and the absolute minimum, if it exists.
-
(Multiple Choice)
4.8/5  (32)
(32)
Determine whether the relation represents a function. If it is a function, state the domain and range.
-
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem.
-A wire of length 3x is bent into the shape of a square. Express the area A of the square as a function of x. A)
B)
C)
D)
(Multiple Choice)
4.8/5  (38)
(38)
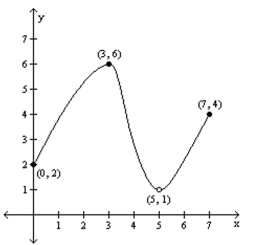
For the graph of the function y = f(x), find the absolute maximum and the absolute minimum, if it exists.
-
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-Sue wants to put a rectangular garden on her property using 76 meters of fencing. There is a river that runs through her property so she decides to increase the size of the garden by using the river as one side of the
Rectangle. (Fencing is then needed only on the other three sides.) Let x represent the length of the side of the
Rectangle along the river. Express the garden's area as a function of x. A)
B)
C)
D)
(Multiple Choice)
4.8/5  (45)
(45)
If y varies directly as x, find a linear function which relates them.
-
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-The height s of a ball (in feet) thrown with an initial velocity of 60 feet per second from an initial height of 4 feet is given as a function of time (in seconds) by . What is the maximum height? Round to the nearest hundredth, if necessary.
(Multiple Choice)
4.8/5  (36)
(36)
Answer the question about the given function.
-Given the function , if , what is ? What point is on the graph of ?
(Multiple Choice)
4.8/5  (44)
(44)
The graph of a function is given. Determine whether the function is increasing, decreasing, or constant on the given
interval.
-
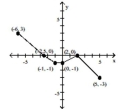
(Multiple Choice)
4.7/5  (34)
(34)
Match the function with the graph that best describes the situation.
-A steel can in the shape of a right circular cylinder must be designed to hold 550 cubic centimeters of juice (see figure). It can be shown that the total surface area of the can (including the ends) is given by S(r) where r is the radius of the can in centimeters. Using the TABLE feature of a graphing utility, find the radius
That minimizes the surface area (and thus the cost) of the can. Round to the nearest tenth of a centimeter. 
(Multiple Choice)
4.8/5  (37)
(37)
Showing 21 - 40 of 301
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)