Exam 1: Functions and Their Graphs
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
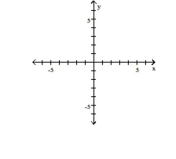
(Multiple Choice)
4.8/5  (35)
(35)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
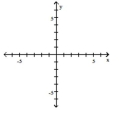 A)
A)
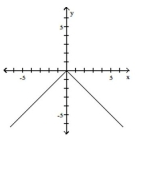 B)
B)
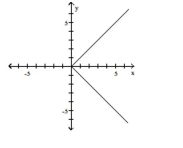 C)
C)
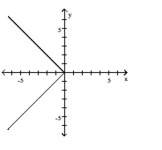 D)
D)
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem.
-A retail store buys 120 VCRs from a distributor at a cost of $200 each plus an overhead charge of $35 per order. The retail markup is 30% on the total price paid. Find the profit on the sale of one VCR.
(Multiple Choice)
4.8/5  (37)
(37)
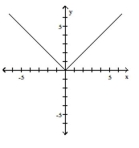
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
(Multiple Choice)
4.8/5  (33)
(33)
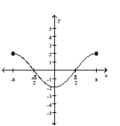
The graph of a function is given. Decide whether it is even, odd, or neither.
-
(Multiple Choice)
4.9/5  (36)
(36)
Find the average rate of change for the function between the given values.
-
(Multiple Choice)
4.8/5  (40)
(40)
Choose the one alternative that best completes the statement or answers the question.
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
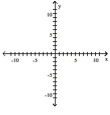 A)
A)
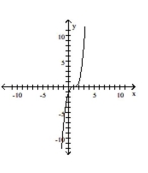 B)
B)
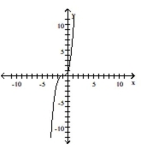 C)
C)
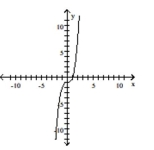 D)
D)
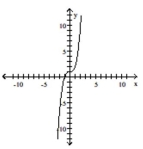
(Multiple Choice)
4.8/5  (33)
(33)
Solve the problem.
-A farmer's silo is the shape of a cylinder with a hemisphere as the roof. If the radius of the hemisphere is 10 feet and the height of the silo is h feet, express the volume of the silo as a function of h. A)
B)
C)
D)
(Multiple Choice)
4.8/5  (42)
(42)
Determine algebraically whether the function is even, odd, or neither.
-
(Multiple Choice)
4.9/5  (35)
(35)
Find and simplify the difference quotient of f, , for the function.
-f(x) = 5x - 8 A) 0
B)
C) 5
D)
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem.
-A farmer has 1,600 yards of fencing to enclose a rectangular garden. Express the area A of the rectangle as a function of the width x of the rectangle. What is the domain of A? A)
B)
C)
D)
(Multiple Choice)
4.9/5  (41)
(41)
The graph of a function is given. Determine whether the function is increasing, decreasing, or constant on the given
interval.
-
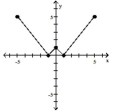
(Multiple Choice)
4.9/5  (31)
(31)
Find the function.
-Find the function that is finally graphed after the following transformations are applied to the graph of The graph is shifted down 3 units, reflected about the x-axis, and finally shifted left 2 units. A)
B)
C)
D)
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-A rectangular box with volume 433 cubic feet is built with a square base and top. The cost is $1.50 per square foot for the top and the bottom and $2.00 per square foot for the sides. Let x represent the length of a side of the
Base. Express the cost the box as a function of x. A)
B)
C)
D)
(Multiple Choice)
4.9/5  (34)
(34)
Solve.
-If the resistance in an electrical circuit is held constant, the amount of current flowing through the circuit varies directly with the amount of voltage applied to the circuit. When 2 volts are applied to a circuit, 40 milliamperes
Of current flow through the circuit. Find the new current if the voltage is increased to 15 volts.
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-The figure shown here shows a rectangle inscribed in an isosceles right triangle whose hypotenuse is 4 units long. Express the area A of the rectangle in terms of x. 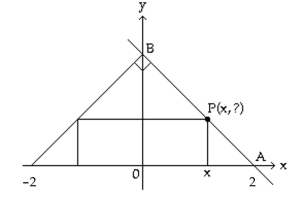
(Multiple Choice)
4.8/5  (29)
(29)
Showing 221 - 240 of 301
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)