Exam 1: Functions and Their Graphs
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Find the average rate of change for the function between the given values.
- from 2 to 8
(Multiple Choice)
4.9/5  (41)
(41)
Suppose the point (2, 4) is on the graph of y = f(x). Find a point on the graph of the given function.
-
(Multiple Choice)
4.8/5  (27)
(27)
Determine whether the equation defines y as a function of x.
-
(Multiple Choice)
5.0/5  (37)
(37)
Determine algebraically whether the function is even, odd, or neither.
-
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem.
-If a rock falls from a height of 80 meters on Earth, the height H (in meters) after x seconds is approximately What is the height of the rock when x = 1.5 seconds? Round to the nearest hundredth, if necessary.
(Multiple Choice)
4.8/5  (38)
(38)
Determine algebraically whether the function is even, odd, or neither.
-
(Multiple Choice)
4.8/5  (35)
(35)
Answer the question about the given function.
-Given the function , list the -intercepts, if any, of the graph of .
(Multiple Choice)
5.0/5  (40)
(40)
Use a graphing utility to graph the function over the indicated interval and approximate any local maxima and local
minima. Determine where the function is increasing and where it is decreasing. If necessary, round answers to two
decimal places.
-
(Essay)
4.8/5  (35)
(35)
Find the average rate of change for the function between the given values.
- ; from 3 to 7
(Multiple Choice)
4.7/5  (44)
(44)
Solve the problem.
-The amount of time it takes a swimmer to swim a race is inversely proportional to the average speed of the swimmer. A swimmer finishes a race in 30 seconds with an average speed of 5 feet per second. Find the average
Speed of the swimmer if it takes 25 seconds to finish the race.
(Multiple Choice)
4.8/5  (37)
(37)
Use a graphing utility to graph the function over the indicated interval and approximate any local maxima and local
minima. If necessary, round answers to two decimal places.
-
(Multiple Choice)
4.9/5  (41)
(41)
Solve.
-The time in hours it takes a satellite to complete an orbit around the earth varies directly as the radius of the orbit (from the center of the earth) and inversely as the orbital velocity. If a satellite completes an orbit 890 miles
Above the earth in 17 hours at a velocity of 21,000 mph, how long would it take a satellite to complete an orbit if
It is at 1,700 miles above the earth at a velocity of 25,000 mph? (Use 3960 miles as the radius of the earth.)
(Multiple Choice)
4.9/5  (34)
(34)
The graph of a piecewise-defined function is given. Write a definition for the function.
-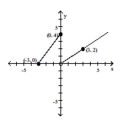 A)
B)
C)
D)
A)
B)
C)
D)
(Multiple Choice)
4.9/5  (25)
(25)
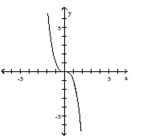
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
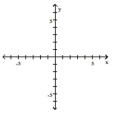 A)
A)
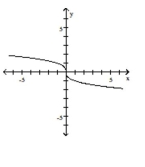 B)
B)
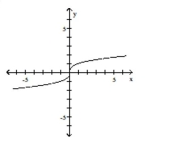 C)
C)
 D)
D)
(Multiple Choice)
4.9/5  (40)
(40)
Solve.
-The voltage across a resistor is jointly proportional to the resistance of the resistor and the current flowing through the resistor. If the voltage across a resistor is 21 volts for a resistor whose resistance is 3 ohms and when
The current flowing through the resistor is 7 amperes, find the voltage across a resistor whose resistance is
2 ohms and when the current flowing through the resistor is 4 amperes.
(Multiple Choice)
4.9/5  (36)
(36)
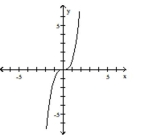
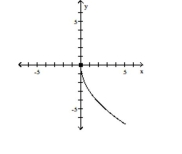
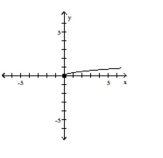
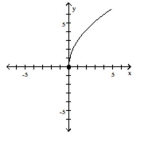
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
 A)
A)
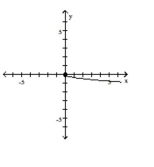 B)
B)
 C)
C)
 D)
D)
(Multiple Choice)
4.8/5  (28)
(28)
Find and simplify the difference quotient of f, , for the function.
-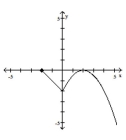 A)
function domain: \{x\midx\leq0\} range: \{y\midy\geq-2\} intercepts: (-2,0),(0,-2),(2,0) symmetry: y -axis
B)
function
domain:
range:
intercepts:
symmetry: none
C)
function
domain: all real numbers
range: all real numbers
intercepts:
symmetry: none
D) not a function
A)
function domain: \{x\midx\leq0\} range: \{y\midy\geq-2\} intercepts: (-2,0),(0,-2),(2,0) symmetry: y -axis
B)
function
domain:
range:
intercepts:
symmetry: none
C)
function
domain: all real numbers
range: all real numbers
intercepts:
symmetry: none
D) not a function
(Multiple Choice)
4.9/5  (35)
(35)
The graph of a function f is given. Use the graph to answer the question.
-Find the numbers, if any, at which f has a local maximum. What are the local maxima? 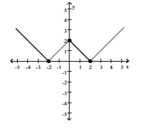
(Multiple Choice)
4.9/5  (36)
(36)
Showing 161 - 180 of 301
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)