Exam 1: Functions and Their Graphs
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Find and simplify the difference quotient of f, , for the function.
-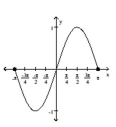 A)
function domain: \{x\mid-\pi\leqx\leq\pi\} range: \{y\mid-1\leqy\leq1\} intercepts: (-\pi,0),(0,0),(\pi,0) symmetry: origin
B)
function
domain: all real numbers
range:
intercepts:
symmetry: origin
C)
function
domain:
range:
intercepts:
symmetry: none
D) not function
A)
function domain: \{x\mid-\pi\leqx\leq\pi\} range: \{y\mid-1\leqy\leq1\} intercepts: (-\pi,0),(0,0),(\pi,0) symmetry: origin
B)
function
domain: all real numbers
range:
intercepts:
symmetry: origin
C)
function
domain:
range:
intercepts:
symmetry: none
D) not function
(Multiple Choice)
4.9/5  (30)
(30)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
 A)
A)
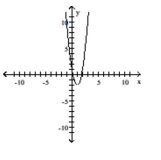 B)
B)
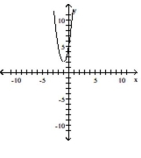 C)
C)
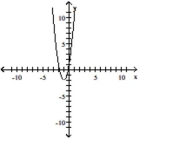 D)
D)
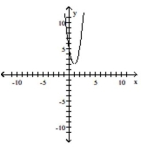
(Multiple Choice)
4.9/5  (31)
(31)
Determine whether the relation represents a function. If it is a function, state the domain and range.
- 4 \rightarrow8 9 \rightarrow18 14 \rightarrow28 19 \rightarrow38
(Multiple Choice)
4.8/5  (27)
(27)
Answer the question about the given function.
-Given the functi , is the point (1, -12) on the graph of f?
(Multiple Choice)
4.8/5  (32)
(32)
Use a graphing utility to graph the function over the indicated interval and approximate any local maxima and local
minima. If necessary, round answers to two decimal places.
-
(Multiple Choice)
4.7/5  (41)
(41)
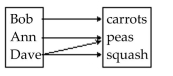
Determine whether the relation represents a function. If it is a function, state the domain and range.
-
(Multiple Choice)
4.8/5  (33)
(33)
Solve the problem.
-Let be a point on the graph of . Express the distance from to the point as a function of
(Multiple Choice)
4.8/5  (29)
(29)
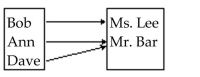
Determine whether the relation represents a function. If it is a function, state the domain and range.
-
(Multiple Choice)
4.9/5  (40)
(40)
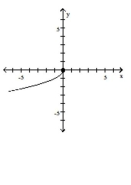
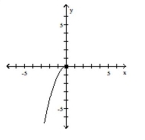
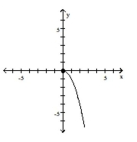
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
 A)
A)
 B)
B)
 C)
C)
 D)
D)
(Multiple Choice)
4.8/5  (39)
(39)
Find the average rate of change for the function between the given values.
-
(Multiple Choice)
4.9/5  (35)
(35)
Use the graph to find the intervals on which it is increasing, decreasing, or constant.
-
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-A wire 20 feet long is to be cut into two pieces. One piece will be shaped as a square and the other piece will be
shaped as an equilateral triangle. Express the total area A enclosed by the pieces of wire as a function of the
length x of a side of the equilateral triangle. What is the domain of A?
(Essay)
4.9/5  (32)
(32)
For the graph of the function y = f(x), find the absolute maximum and the absolute minimum, if it exists.
-
(Multiple Choice)
4.8/5  (36)
(36)
Answer the question about the given function.
-Given the function , what is the domain of ?
(Multiple Choice)
4.8/5  (34)
(34)
The graph of a function is given. Decide whether it is even, odd, or neither.
-
(Multiple Choice)
4.7/5  (32)
(32)
Solve the problem.
-The price and , the quantity of a certain product sold, obey the demand equation
a) Express the revenue as a function of .
b) What is the revenue if 450 units are sold?
c) Graph the revenue function using a graphing utility.
d) What quantity x maximizes revenue? What is the maximum revenue?
e) What price should the company charge to maximize revenue?
(Essay)
4.9/5  (29)
(29)
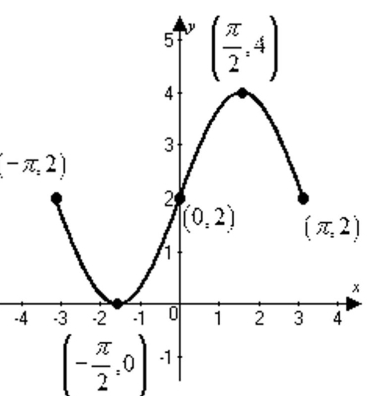
Use the graph to find the intervals on which it is increasing, decreasing, or constant.
-
(Multiple Choice)
4.9/5  (38)
(38)
Showing 101 - 120 of 301
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)